Venn GAN: Discovering Commonalities and Particularities of Multiple Distributions

We propose a GAN design which models multiple distributions effectively and discovers their commonalities and particularities. Each data distribution is modeled with a mixture of $K$ generator distributions. As the generators are partially shared between the modeling of different true data distributions, shared ones captures the commonality of the distributions, while non-shared ones capture unique aspects of them. We show the effectiveness of our method on various datasets (MNIST, Fashion MNIST, CIFAR-10, Omniglot, CelebA) with compelling results.

The Unusual Effectiveness of Averaging in GAN Training

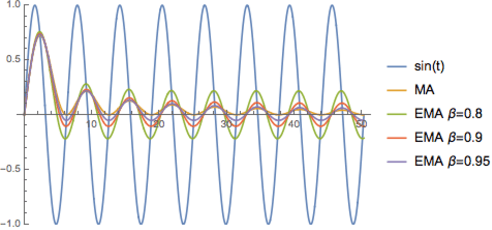
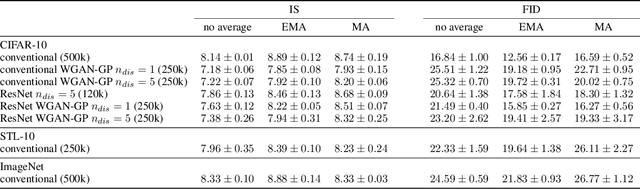
We show empirically that the optimal strategy of parameter averaging in a minmax convex-concave game setting is also strikingly effective in the non convex-concave GAN setting, specifically alleviating the convergence issues associated with cycling behavior observed in GANs. We show that averaging over generator parameters outside of the trainig loop consistently improves inception and FID scores on different architectures and for different GAN objectives. We provide comprehensive experimental results across a range of datasets, bilinear games, mixture of Gaussians, CIFAR-10, STL-10, CelebA and ImageNet, to demonstrate its effectiveness. We achieve state-of-the-art results on CIFAR-10 and produce clean CelebA face images, demonstrating that averaging is one of the most effective techniques for training highly performant GANs.