Yantao Gong
Confidence Calibration for Intent Detection via Hyperspherical Space and Rebalanced Accuracy-Uncertainty Loss
Mar 17, 2022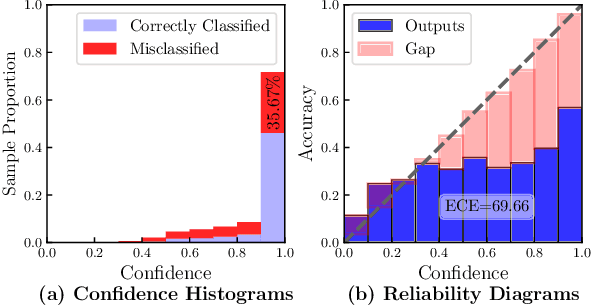
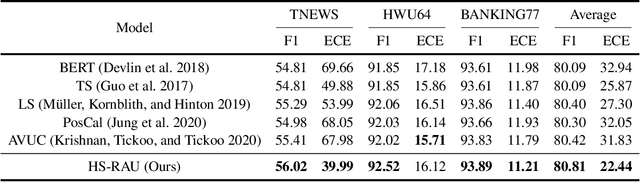
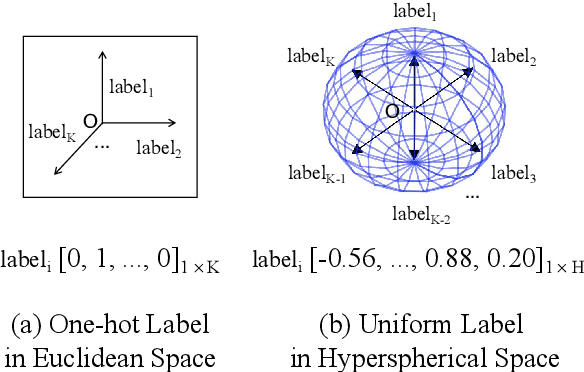
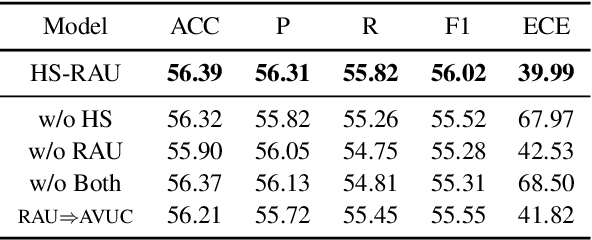
Abstract:Data-driven methods have achieved notable performance on intent detection, which is a task to comprehend user queries. Nonetheless, they are controversial for over-confident predictions. In some scenarios, users do not only care about the accuracy but also the confidence of model. Unfortunately, mainstream neural networks are poorly calibrated, with a large gap between accuracy and confidence. To handle this problem defined as confidence calibration, we propose a model using the hyperspherical space and rebalanced accuracy-uncertainty loss. Specifically, we project the label vector onto hyperspherical space uniformly to generate a dense label representation matrix, which mitigates over-confident predictions due to overfitting sparce one-hot label matrix. Besides, we rebalance samples of different accuracy and uncertainty to better guide model training. Experiments on the open datasets verify that our model outperforms the existing calibration methods and achieves a significant improvement on the calibration metric.
Density-Based Dynamic Curriculum Learning for Intent Detection
Aug 24, 2021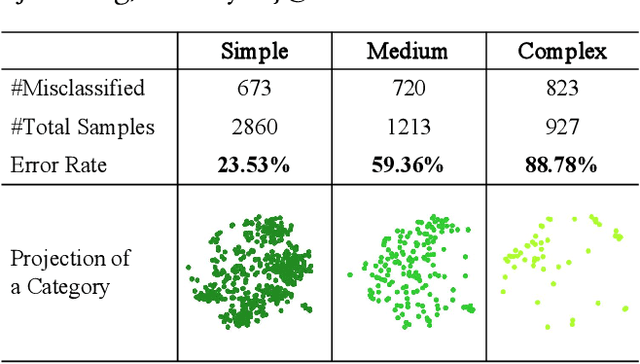

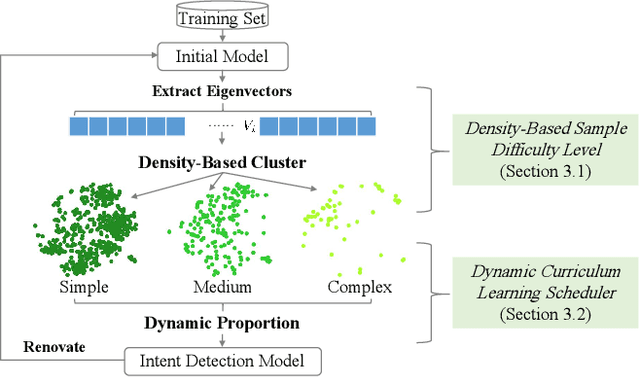
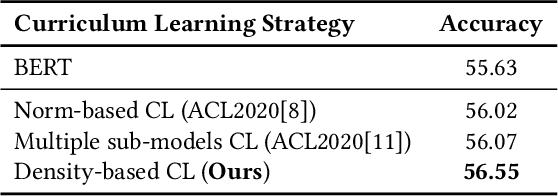
Abstract:Pre-trained language models have achieved noticeable performance on the intent detection task. However, due to assigning an identical weight to each sample, they suffer from the overfitting of simple samples and the failure to learn complex samples well. To handle this problem, we propose a density-based dynamic curriculum learning model. Our model defines the sample's difficulty level according to their eigenvectors' density. In this way, we exploit the overall distribution of all samples' eigenvectors simultaneously. Then we apply a dynamic curriculum learning strategy, which pays distinct attention to samples of various difficulty levels and alters the proportion of samples during the training process. Through the above operation, simple samples are well-trained, and complex samples are enhanced. Experiments on three open datasets verify that the proposed density-based algorithm can distinguish simple and complex samples significantly. Besides, our model obtains obvious improvement over the strong baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge