Epistemic Syllogistic: First Steps

Aristotle's discussions on modal syllogistic have often been viewed as error-prone and have garnered significant attention in the literature due to historical and philosophical interests. However, from a contemporary standpoint, they also introduced natural fragments of first-order modal logic, warranting a comprehensive technical analysis. In this paper, drawing inspiration from the natural logic program, we propose and examine several variants of modal syllogistic within the epistemic context, thereby coining the term Epistemic Syllogistic. Specifically, we concentrate on the de re interpretation of epistemic syllogisms containing non-trivial yet natural expressions such as "all things known to be A are also known to be not B." We explore the epistemic apodeictic syllogistic and its extensions, which accommodate more complex terms. Our main contributions include several axiomatizations of these logics, with completeness proofs that may be of independent interest.

Knowing How to Plan

Various planning-based know-how logics have been studied in the recent literature. In this paper, we use such a logic to do know-how-based planning via model checking. In particular, we can handle the higher-order epistemic planning involving know-how formulas as the goal, e.g., find a plan to make sure p such that the adversary does not know how to make p false in the future. We give a PTIME algorithm for the model checking problem over finite epistemic transition systems and axiomatize the logic under the assumption of perfect recall.

De Re Updates

In this paper, we propose a lightweight yet powerful dynamic epistemic logic that captures not only the distinction between de dicto and de re knowledge but also the distinction between de dicto and de re updates. The logic is based on the dynamified version of an epistemic language extended with the assignment operator borrowed from dynamic logic, following the work of Wang and Seligman (Proc. AiML 2018). We obtain complete axiomatizations for the counterparts of public announcement logic and event-model-based DEL based on new reduction axioms taking care of the interactions between dynamics and assignments.

Weakly Aggregative Modal Logic: Characterization and Interpolation

In this paper, we study the model theoretical aspects of Weakly Aggregative Modal Logic (WAL), which is a collection of disguised polyadic modal logics with $n$-ary modalities whose arguments are all the same. We give a van-Benthem-Rosen characterization theorem of WAL based on an intuitive notion of bisimulation, and show that WAL has Craig Interpolation.

When Names Are Not Commonly Known: Epistemic Logic with Assignments

In standard epistemic logic, agent names are usually assumed to be common knowledge implicitly. This is unreasonable for various applications. Inspired by term modal logic and assignment operators in dynamic logic, we introduce a lightweight modal predicate logic where names can be non-rigid. The language can handle various de dicto and de re distinctions in a natural way. The main technical result is a complete axiomatisation of this logic over S5 models.

Bundled fragments of first-order modal logic: decidability

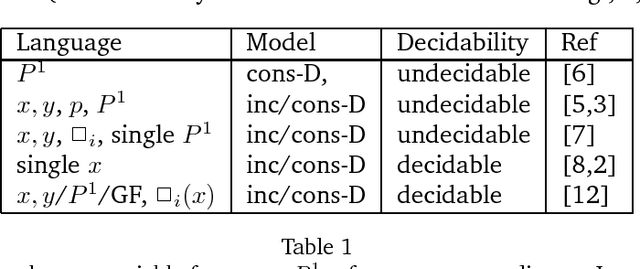
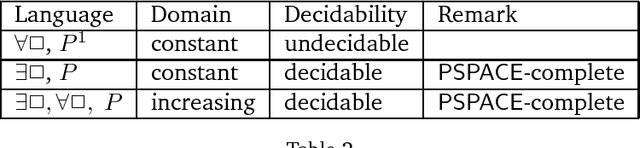
Quantified modal logic provides a natural logical language for reasoning about modal attitudes even while retaining the richness of quantification for referring to predicates over domains. But then most fragments of the logic are undecidable, over many model classes. Over the years, only a few fragments (such as the monodic) have been shown to be decidable. In this paper, we study fragments that bundle quantifiers and modalities together, inspired by earlier work on epistemic logics of know-how/why/what. As always with quantified modal logics, it makes a significant difference whether the domain stays the same across worlds, or not. In particular, we show that the bundle $\forall \Box$ is undecidable over constant domain interpretations, even with only monadic predicates, whereas $\exists \Box$ bundle is decidable. On the other hand, over increasing domain interpretations, we get decidability with both $\forall \Box$ and $\exists \Box$ bundles with unrestricted predicates. In these cases, we also obtain tableau based procedures that run in \PSPACE. We further show that the $\exists \Box$ bundle cannot distinguish between constant domain and increasing domain interpretations.

A New Modal Framework for Epistemic Logic

Recent years witnessed a growing interest in non-standard epistemic logics of knowing whether, knowing how, knowing what, knowing why and so on. The new epistemic modalities introduced in those logics all share, in their semantics, the general schema of $\exists x \Box \phi$, e.g., knowing how to achieve $\phi$ roughly means that there exists a way such that you know that it is a way to ensure that $\phi$. Moreover, the resulting logics are decidable. Inspired by those particular logics, in this work, we propose a very general and powerful framework based on quantifier-free predicate language extended by a new modality $\Box^x$, which packs exactly $\exists x \Box$ together. We show that the resulting language, though much more expressive, shares many good properties of the basic propositional modal logic over arbitrary models, such as finite-tree-model property and van Benthem-like characterization w.r.t.\ first-order modal logic. We axiomatize the logic over S5 frames with intuitive axioms to capture the interaction between $\Box^x$ and know-that operator in an epistemic setting.

Strategically knowing how

In this paper, we propose a single-agent logic of goal-directed knowing how extending the standard epistemic logic of knowing that with a new knowing how operator. The semantics of the new operator is based on the idea that knowing how to achieve $\phi$ means that there exists a (uniform) strategy such that the agent knows that it can make sure $\phi$. We give an intuitive axiomatization of our logic and prove the soundness, completeness, and decidability of the logic. The crucial axioms relating knowing that and knowing how illustrate our understanding of knowing how in this setting. This logic can be used in representing both knowledge-that and knowledge-how.

True Lies

A true lie is a lie that becomes true when announced. In a logic of announcements, where the announcing agent is not modelled, a true lie is a formula (that is false and) that becomes true when announced. We investigate true lies and other types of interaction between announced formulas, their preconditions and their postconditions, in the setting of Gerbrandy's logic of believed announcements, wherein agents may have or obtain incorrect beliefs. Our results are on the satisfiability and validity of instantiations of these semantically defined categories, on iterated announcements, including arbitrarily often iterated announcements, and on syntactic characterization. We close with results for iterated announcements in the logic of knowledge (instead of belief), and for lying as private announcements (instead of public announcements) to different agents. Detailed examples illustrate our lying concepts.

A Logic of Knowing Why

When we say "I know why he was late", we know not only the fact that he was late, but also an explanation of this fact. We propose a logical framework of "knowing why" inspired by the existing formal studies on why-questions, scientific explanation, and justification logic. We introduce the Ky_i operator into the language of epistemic logic to express "agent i knows why phi" and propose a Kripke-style semantics of such expressions in terms of knowing an explanation of phi. We obtain two sound and complete axiomatizations w.r.t. two different model classes depending on different assumptions about introspection.