True Lies

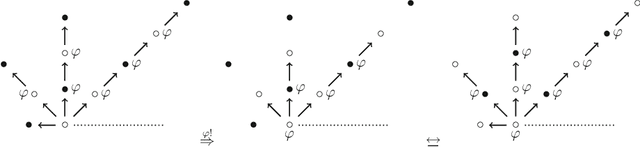
A true lie is a lie that becomes true when announced. In a logic of announcements, where the announcing agent is not modelled, a true lie is a formula (that is false and) that becomes true when announced. We investigate true lies and other types of interaction between announced formulas, their preconditions and their postconditions, in the setting of Gerbrandy's logic of believed announcements, wherein agents may have or obtain incorrect beliefs. Our results are on the satisfiability and validity of instantiations of these semantically defined categories, on iterated announcements, including arbitrarily often iterated announcements, and on syntactic characterization. We close with results for iterated announcements in the logic of knowledge (instead of belief), and for lying as private announcements (instead of public announcements) to different agents. Detailed examples illustrate our lying concepts.

Resolving Distributed Knowledge

Distributed knowledge is the sum of the knowledge in a group; what someone who is able to discern between two possible worlds whenever any member of the group can discern between them, would know. Sometimes distributed knowledge is referred to as the potential knowledge of a group, or the joint knowledge they could obtain if they had unlimited means of communication. In epistemic logic, the formula D_G{\phi} is intended to express the fact that group G has distributed knowledge of {\phi}, that there is enough information in the group to infer {\phi}. But this is not the same as reasoning about what happens if the members of the group share their information. In this paper we introduce an operator R_G, such that R_G{\phi} means that {\phi} is true after G have shared all their information with each other - after G's distributed knowledge has been resolved. The R_G operators are called resolution operators. Semantically, we say that an expression R_G{\phi} is true iff {\phi} is true in what van Benthem [11, p. 249] calls (G's) communication core; the model update obtained by removing links to states for members of G that are not linked by all members of G. We study logics with different combinations of resolution operators and operators for common and distributed knowledge. Of particular interest is the relationship between distributed and common knowledge. The main results are sound and complete axiomatizations.