Minimax Rate-Optimal Algorithms for High-Dimensional Stochastic Linear Bandits

We study the stochastic linear bandit problem with multiple arms over $T$ rounds, where the covariate dimension $d$ may exceed $T$, but each arm-specific parameter vector is $s$-sparse. We begin by analyzing the sequential estimation problem in the single-arm setting, focusing on cumulative mean-squared error. We show that Lasso estimators are provably suboptimal in the sequential setting, exhibiting suboptimal dependence on $d$ and $T$, whereas thresholded Lasso estimators -- obtained by applying least squares to the support selected by thresholding an initial Lasso estimator -- achieve the minimax rate. Building on these insights, we consider the full linear contextual bandit problem and propose a three-stage arm selection algorithm that uses thresholded Lasso as the main estimation method. We derive an upper bound on the cumulative regret of order $s(\log s)(\log d + \log T)$, and establish a matching lower bound up to a $\log s$ factor, thereby characterizing the minimax regret rate up to a logarithmic term in $s$. Moreover, when a short initial period is excluded from the regret, the proposed algorithm achieves exact minimax optimality.

Truncated LinUCB for Stochastic Linear Bandits

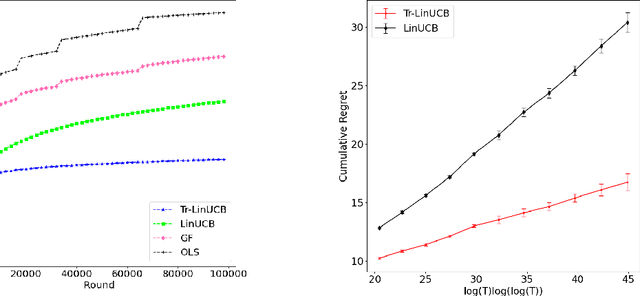
This paper considers contextual bandits with a finite number of arms, where the contexts are independent and identically distributed $d$-dimensional random vectors, and the expected rewards are linear in both the arm parameters and contexts. The LinUCB algorithm, which is near minimax optimal for related linear bandits, is shown to have a cumulative regret that is suboptimal in both the dimension $d$ and time horizon $T$, due to its over-exploration. A truncated version of LinUCB is proposed and termed "Tr-LinUCB", which follows LinUCB up to a truncation time $S$ and performs pure exploitation afterwards. The Tr-LinUCB algorithm is shown to achieve $O(d\log(T))$ regret if $S = Cd\log(T)$ for a sufficiently large constant $C$, and a matching lower bound is established, which shows the rate optimality of Tr-LinUCB in both $d$ and $T$ under a low dimensional regime. Further, if $S = d\log^{\kappa}(T)$ for some $\kappa>1$, the loss compared to the optimal is a multiplicative $\log\log(T)$ factor, which does not depend on $d$. This insensitivity to overshooting in choosing the truncation time of Tr-LinUCB is of practical importance.

Scalable Topical Phrase Mining from Text Corpora

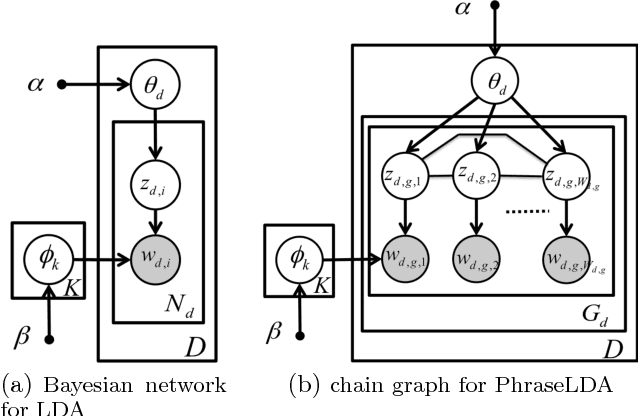
While most topic modeling algorithms model text corpora with unigrams, human interpretation often relies on inherent grouping of terms into phrases. As such, we consider the problem of discovering topical phrases of mixed lengths. Existing work either performs post processing to the inference results of unigram-based topic models, or utilizes complex n-gram-discovery topic models. These methods generally produce low-quality topical phrases or suffer from poor scalability on even moderately-sized datasets. We propose a different approach that is both computationally efficient and effective. Our solution combines a novel phrase mining framework to segment a document into single and multi-word phrases, and a new topic model that operates on the induced document partition. Our approach discovers high quality topical phrases with negligible extra cost to the bag-of-words topic model in a variety of datasets including research publication titles, abstracts, reviews, and news articles.

Scalable and Robust Construction of Topical Hierarchies

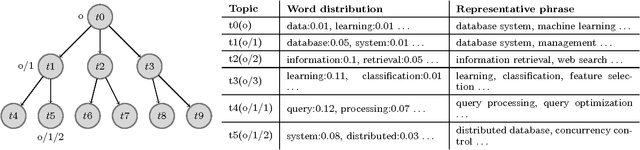
Automated generation of high-quality topical hierarchies for a text collection is a dream problem in knowledge engineering with many valuable applications. In this paper a scalable and robust algorithm is proposed for constructing a hierarchy of topics from a text collection. We divide and conquer the problem using a top-down recursive framework, based on a tensor orthogonal decomposition technique. We solve a critical challenge to perform scalable inference for our newly designed hierarchical topic model. Experiments with various real-world datasets illustrate its ability to generate robust, high-quality hierarchies efficiently. Our method reduces the time of construction by several orders of magnitude, and its robust feature renders it possible for users to interactively revise the hierarchy.