Xinye Chen
Precision Autotuning for Linear Solvers via Reinforcement Learning
Jan 05, 2026Abstract:We propose a reinforcement learning (RL) framework for adaptive precision tuning of linear solvers, and can be extended to general algorithms. The framework is formulated as a contextual bandit problem and solved using incremental action-value estimation with a discretized state space to select optimal precision configurations for computational steps, balancing precision and computational efficiency. To verify its effectiveness, we apply the framework to iterative refinement for solving linear systems $Ax = b$. In this application, our approach dynamically chooses precisions based on calculated features from the system. In detail, a Q-table maps discretized features (e.g., approximate condition number and matrix norm)to actions (chosen precision configurations for specific steps), optimized via an epsilon-greedy strategy to maximize a multi-objective reward balancing accuracy and computational cost. Empirical results demonstrate effective precision selection, reducing computational cost while maintaining accuracy comparable to double-precision baselines. The framework generalizes to diverse out-of-sample data and offers insight into utilizing RL precision selection for other numerical algorithms, advancing mixed-precision numerical methods in scientific computing. To the best of our knowledge, this is the first work on precision autotuning with RL and verified on unseen datasets.
QuantiPhy: A Quantitative Benchmark Evaluating Physical Reasoning Abilities of Vision-Language Models
Dec 22, 2025Abstract:Understanding the physical world is essential for generalist AI agents. However, it remains unclear whether state-of-the-art vision perception models (e.g., large VLMs) can reason physical properties quantitatively. Existing evaluations are predominantly VQA-based and qualitative, offering limited insight into whether these models can infer the kinematic quantities of moving objects from video observations. To address this, we present QuantiPhy, the first benchmark designed to quantitatively measure a VLM's physical reasoning ability. Comprising more than 3.3K video-text instances with numerical ground truth, QuantiPhy evaluates a VLM's performance on estimating an object's size, velocity, and acceleration at a given timestamp, using one of these properties as an input prior. The benchmark standardizes prompts and scoring to assess numerical accuracy, enabling fair comparisons across models. Our experiments on state-of-the-art VLMs reveal a consistent gap between their qualitative plausibility and actual numerical correctness. We further provide an in-depth analysis of key factors like background noise, counterfactual priors, and strategic prompting and find that state-of-the-art VLMs lean heavily on pre-trained world knowledge rather than faithfully using the provided visual and textual inputs as references when reasoning kinematic properties quantitatively. QuantiPhy offers the first rigorous, scalable testbed to move VLMs beyond mere verbal plausibility toward a numerically grounded physical understanding.
Mixed-Precision Conjugate Gradient Solvers with RL-Driven Precision Tuning
Apr 19, 2025Abstract:This paper presents a novel reinforcement learning (RL) framework for dynamically optimizing numerical precision in the preconditioned conjugate gradient (CG) method. By modeling precision selection as a Markov Decision Process (MDP), we employ Q-learning to adaptively assign precision levels to key operations, striking an optimal balance between computational efficiency and numerical accuracy, while ensuring stability through double-precision scalar computations and residual computing. In practice, the algorithm is trained on a set of data and subsequently performs inference for precision selection on out-of-sample data, without requiring re-analysis or retraining for new datasets. This enables the method to adapt seamlessly to new problem instances without the computational overhead of recalibration. Our results demonstrate the effectiveness of RL in enhancing solver's performance, marking the first application of RL to mixed-precision numerical methods. The findings highlight the approach's practical advantages, robustness, and scalability, providing valuable insights into its integration with iterative solvers and paving the way for AI-driven advancements in scientific computing.
Pychop: Emulating Low-Precision Arithmetic in Numerical Methods and Neural Networks
Apr 10, 2025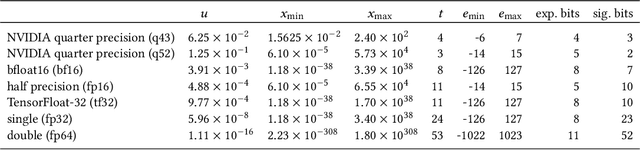
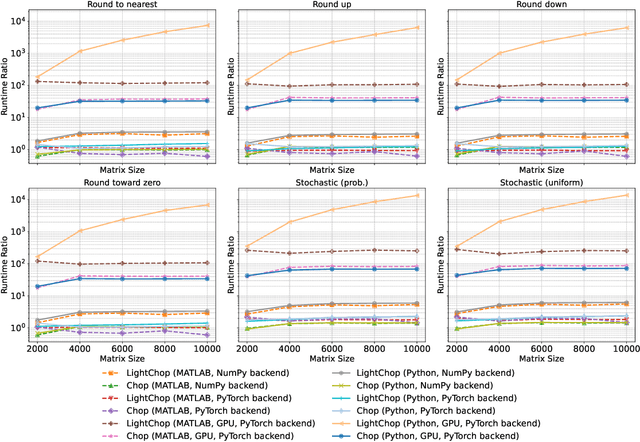
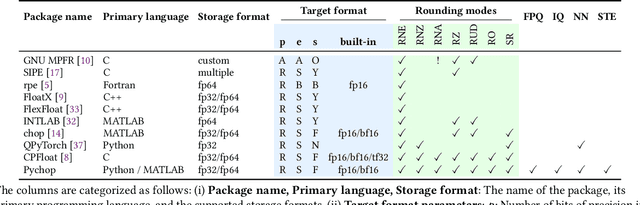
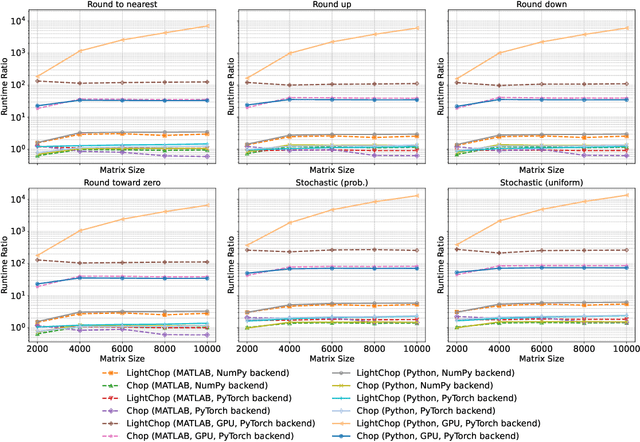
Abstract:Motivated by the growing demand for low-precision arithmetic in computational science, we exploit lower-precision emulation in Python -- widely regarded as the dominant programming language for numerical analysis and machine learning. Low-precision training has revolutionized deep learning by enabling more efficient computation and reduced memory and energy consumption while maintaining model fidelity. To better enable numerical experimentation with and exploration of low precision computation, we developed the Pychop library, which supports customizable floating-point formats and a comprehensive set of rounding modes in Python, allowing users to benefit from fast, low-precision emulation in numerous applications. Pychop also introduces interfaces for both PyTorch and JAX, enabling efficient low-precision emulation on GPUs for neural network training and inference with unparalleled flexibility. In this paper, we offer a comprehensive exposition of the design, implementation, validation, and practical application of Pychop, establishing it as a foundational tool for advancing efficient mixed-precision algorithms. Furthermore, we present empirical results on low-precision emulation for image classification and object detection using published datasets, illustrating the sensitivity of the use of low precision and offering valuable insights into its impact. Pychop enables in-depth investigations into the effects of numerical precision, facilitates the development of novel hardware accelerators, and integrates seamlessly into existing deep learning workflows. Software and experimental code are publicly available at https://github.com/inEXASCALE/pychop.
LLM-ABBA: Understanding time series via symbolic approximation
Dec 03, 2024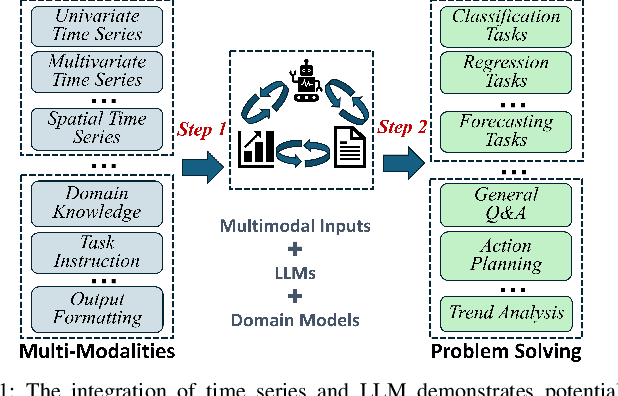
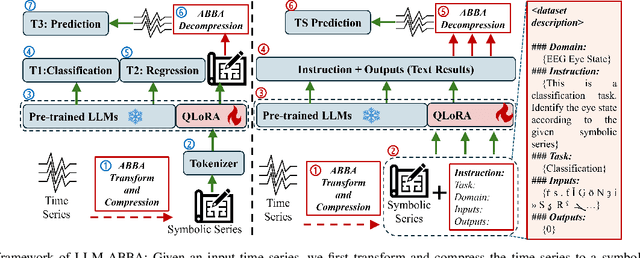
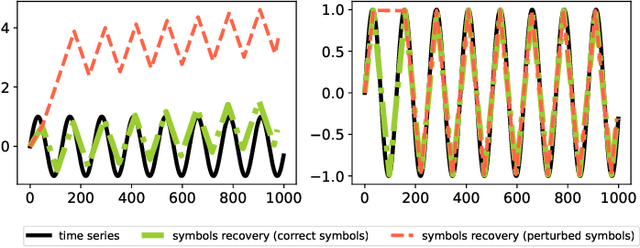
Abstract:The success of large language models (LLMs) for time series has been demonstrated in previous work. Utilizing a symbolic time series representation, one can efficiently bridge the gap between LLMs and time series. However, the remaining challenge is to exploit the semantic information hidden in time series by using symbols or existing tokens of LLMs, while aligning the embedding space of LLMs according to the hidden information of time series. The symbolic time series approximation (STSA) method called adaptive Brownian bridge-based symbolic aggregation (ABBA) shows outstanding efficacy in preserving salient time series features by modeling time series patterns in terms of amplitude and period while using existing tokens of LLMs. In this paper, we introduce a method, called LLM-ABBA, that integrates ABBA into large language models for various downstream time series tasks. By symbolizing time series, LLM-ABBA compares favorably to the recent state-of-the-art (SOTA) in UCR and three medical time series classification tasks. Meanwhile, a fixed-polygonal chain trick in ABBA is introduced to \kc{avoid obvious drifting} during prediction tasks by significantly mitigating the effects of cumulative error arising from misused symbols during the transition from symbols to numerical values. In time series regression tasks, LLM-ABBA achieves the new SOTA on Time Series Extrinsic Regression (TSER) benchmarks. LLM-ABBA also shows competitive prediction capability compared to recent SOTA time series prediction results. We believe this framework can also seamlessly extend to other time series tasks.
Quantized symbolic time series approximation
Nov 20, 2024Abstract:Time series are ubiquitous in numerous science and engineering domains, e.g., signal processing, bioinformatics, and astronomy. Previous work has verified the efficacy of symbolic time series representation in a variety of engineering applications due to its storage efficiency and numerosity reduction. The most recent symbolic aggregate approximation technique, ABBA, has been shown to preserve essential shape information of time series and improve downstream applications, e.g., neural network inference regarding prediction and anomaly detection in time series. Motivated by the emergence of high-performance hardware which enables efficient computation for low bit-width representations, we present a new quantization-based ABBA symbolic approximation technique, QABBA, which exhibits improved storage efficiency while retaining the original speed and accuracy of symbolic reconstruction. We prove an upper bound for the error arising from quantization and discuss how the number of bits should be chosen to balance this with other errors. An application of QABBA with large language models (LLMs) for time series regression is also presented, and its utility is investigated. By representing the symbolic chain of patterns on time series, QABBA not only avoids the training of embedding from scratch, but also achieves a new state-of-the-art on Monash regression dataset. The symbolic approximation to the time series offers a more efficient way to fine-tune LLMs on the time series regression task which contains various application domains. We further present a set of extensive experiments performed across various well-established datasets to demonstrate the advantages of the QABBA method for symbolic approximation.
Quantized Embedding Vectors for Controllable Diffusion Language Models
Feb 15, 2024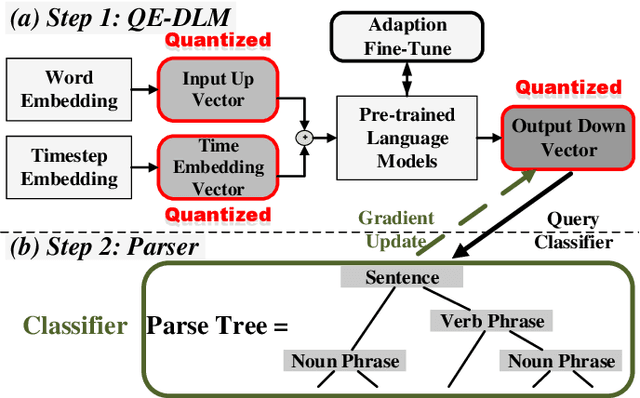

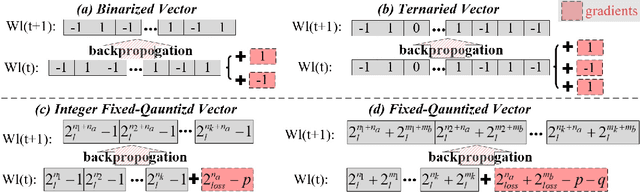
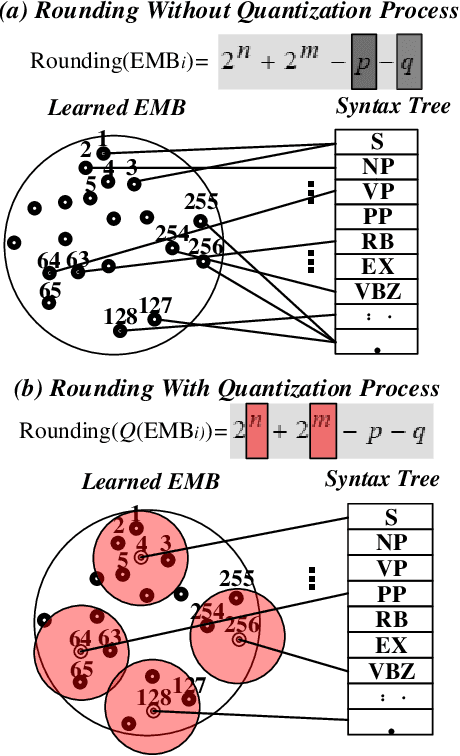
Abstract:Improving the controllability, portability, and inference speed of diffusion language models (DLMs) is a key challenge in natural language generation. While recent research has shown significant success in complex text generation with language models, the memory and computational power are still very demanding and fall short of expectations, which naturally results in low portability and instability for the models. To mitigate these issues, numerous well-established methods were proposed for neural network quantization. To further enhance their portability of independent deployment as well as improve their stability evaluated by language perplexity, we propose a novel approach called the Quantized Embedding Controllable Diffusion Language Model (QE-CDLM). QE-CDLM builds upon the recent successful controllable DLMs by remodeling the task-specific embedding space via quantization. This leads to a gradient-based controller for the generation tasks, and more stable intermediate latent variables are obtained, which naturally brings in an accelerated convergence as well as better controllability. Additionally, the adaption fine-tuning method is employed to reduce tunable weights. Experimental results on five challenging fine-grained control tasks demonstrate that QE-CDLM compares favorably to existing methods in terms of quality and feasibility, achieving better perplexity and lightweight fine-tuning.
Exact fixed-radius nearest neighbor search with an application to clustering
Dec 15, 2022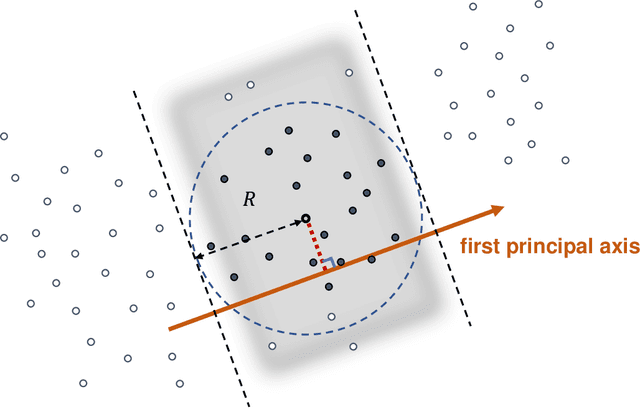
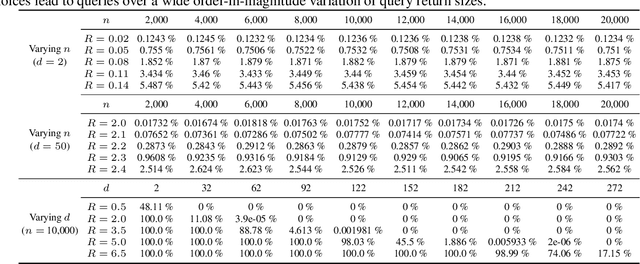
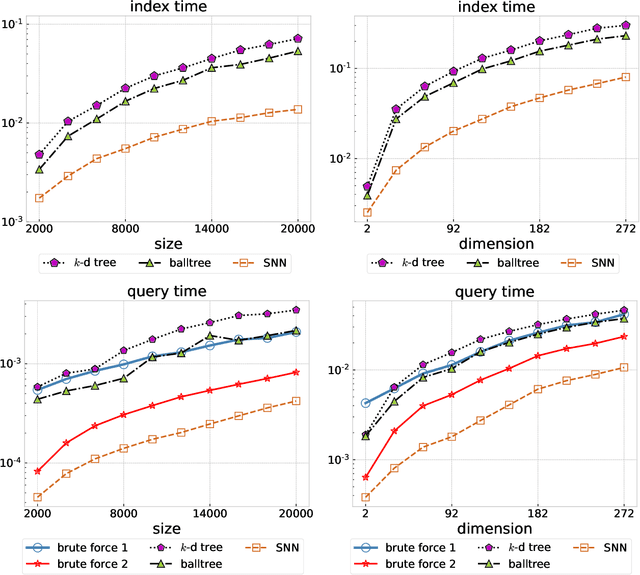
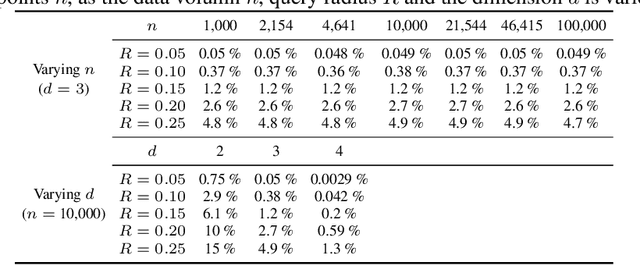
Abstract:Fixed-radius nearest-neighbor search is a common database operation that retrieves all data points within a user-specified distance to a query point. There are efficient approximate nearest neighbor search algorithms that provide fast query responses but they often have a very compute-intensive indexing phase and require parameter tuning. Therefore, exact brute force and tree-based search methods are still widely used. Here we propose a new fixed-radius nearest neighbor search method that significantly improves over brute force and tree-based methods in terms of index and query time, returns exact results, and requires no parameter tuning. The method exploits a sorting of the data points by their first principal component, thereby facilitating a reduction in query search space. Further speedup is gained from an efficient implementation using high-level Basic Linear Algebra Subprograms (BLAS). We provide theoretical analysis of our method and demonstrate its practical performance when used stand-alone and when applied within a clustering algorithm.
Fast and explainable clustering based on sorting
Feb 03, 2022
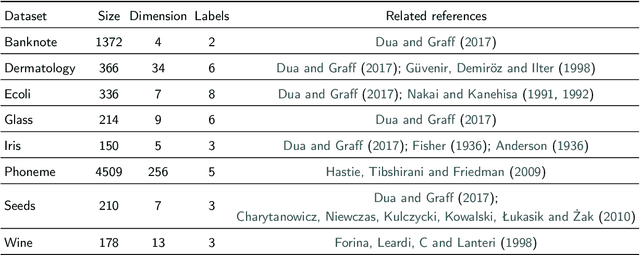


Abstract:We introduce a fast and explainable clustering method called CLASSIX. It consists of two phases, namely a greedy aggregation phase of the sorted data into groups of nearby data points, followed by the merging of groups into clusters. The algorithm is controlled by two scalar parameters, namely a distance parameter for the aggregation and another parameter controlling the minimal cluster size. Extensive experiments are conducted to give a comprehensive evaluation of the clustering performance on synthetic and real-world datasets, with various cluster shapes and low to high feature dimensionality. Our experiments demonstrate that CLASSIX competes with state-of-the-art clustering algorithms. The algorithm has linear space complexity and achieves near linear time complexity on a wide range of problems. Its inherent simplicity allows for the generation of intuitive explanations of the computed clusters.
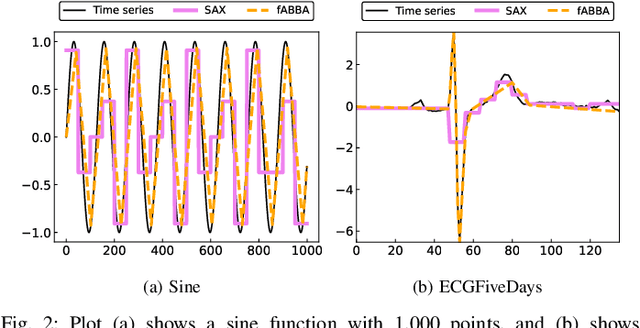
An efficient aggregation method for the symbolic representation of temporal data
Jan 14, 2022



Abstract:Symbolic representations are a useful tool for the dimension reduction of temporal data, allowing for the efficient storage of and information retrieval from time series. They can also enhance the training of machine learning algorithms on time series data through noise reduction and reduced sensitivity to hyperparameters. The adaptive Brownian bridge-based aggregation (ABBA) method is one such effective and robust symbolic representation, demonstrated to accurately capture important trends and shapes in time series. However, in its current form the method struggles to process very large time series. Here we present a new variant of the ABBA method, called fABBA. This variant utilizes a new aggregation approach tailored to the piecewise representation of time series. By replacing the k-means clustering used in ABBA with a sorting-based aggregation technique, and thereby avoiding repeated sum-of-squares error computations, the computational complexity is significantly reduced. In contrast to the original method, the new approach does not require the number of time series symbols to be specified in advance. Through extensive tests we demonstrate that the new method significantly outperforms ABBA with a considerable reduction in runtime while also outperforming the popular SAX and 1d-SAX representations in terms of reconstruction accuracy. We further demonstrate that fABBA can compress other data types such as images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge