Inverse-Free Fast Natural Gradient Descent Method for Deep Learning

Second-order methods can converge much faster than first-order methods by incorporating second-order derivates or statistics, but they are far less prevalent in deep learning due to their computational inefficiency. To handle this, many of the existing solutions focus on reducing the size of the matrix to be inverted. However, it is still needed to perform the inverse operator in each iteration. In this paper, we present a fast natural gradient descent (FNGD) method, which only requires computing the inverse during the first epoch. Firstly, we reformulate the gradient preconditioning formula in the natural gradient descent (NGD) as a weighted sum of per-sample gradients using the Sherman-Morrison-Woodbury formula. Building upon this, to avoid the iterative inverse operation involved in computing coefficients, the weighted coefficients are shared across epochs without affecting the empirical performance. FNGD approximates the NGD as a fixed-coefficient weighted sum, akin to the average sum in first-order methods. Consequently, the computational complexity of FNGD can approach that of first-order methods. To demonstrate the efficiency of the proposed FNGD, we perform empirical evaluations on image classification and machine translation tasks. For training ResNet-18 on the CIFAR-100 dataset, FNGD can achieve a speedup of 2.05$\times$ compared with KFAC. For training Transformer on Multi30K, FNGD outperforms AdamW by 24 BLEU score while requiring almost the same training time.

Low Rank Optimization for Efficient Deep Learning: Making A Balance between Compact Architecture and Fast Training

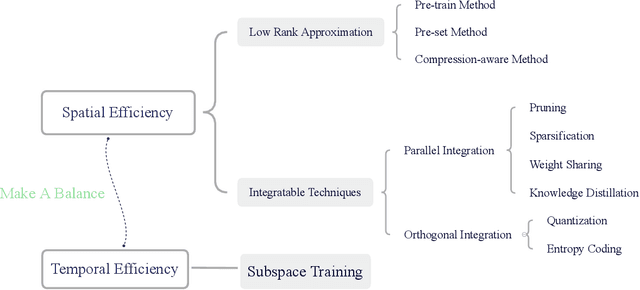
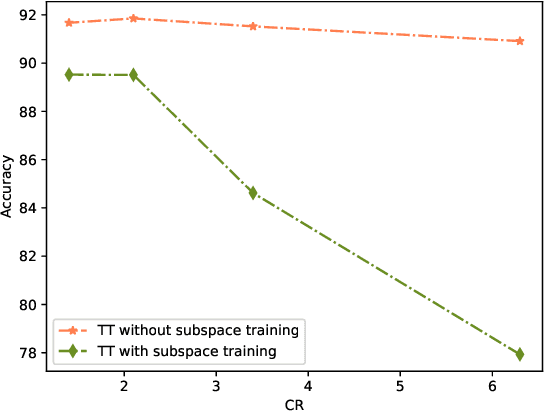
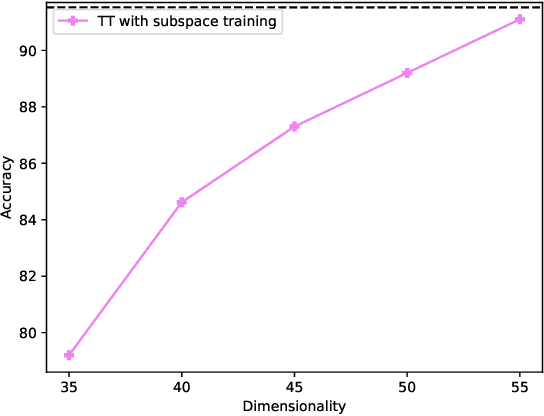
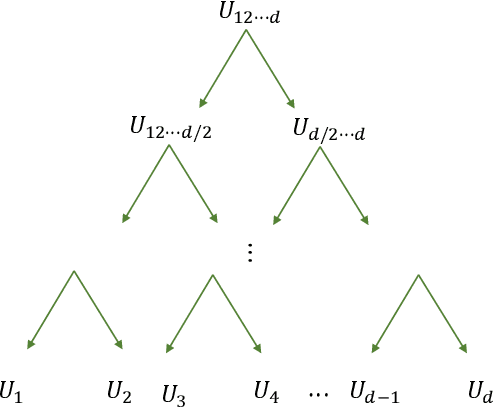
Deep neural networks have achieved great success in many data processing applications. However, the high computational complexity and storage cost makes deep learning hard to be used on resource-constrained devices, and it is not environmental-friendly with much power cost. In this paper, we focus on low-rank optimization for efficient deep learning techniques. In the space domain, deep neural networks are compressed by low rank approximation of the network parameters, which directly reduces the storage requirement with a smaller number of network parameters. In the time domain, the network parameters can be trained in a few subspaces, which enables efficient training for fast convergence. The model compression in the spatial domain is summarized into three categories as pre-train, pre-set, and compression-aware methods, respectively. With a series of integrable techniques discussed, such as sparse pruning, quantization, and entropy coding, we can ensemble them in an integration framework with lower computational complexity and storage. Besides of summary of recent technical advances, we have two findings for motivating future works: one is that the effective rank outperforms other sparse measures for network compression. The other is a spatial and temporal balance for tensorized neural networks.