PromptGCN: Bridging Subgraph Gaps in Lightweight GCNs

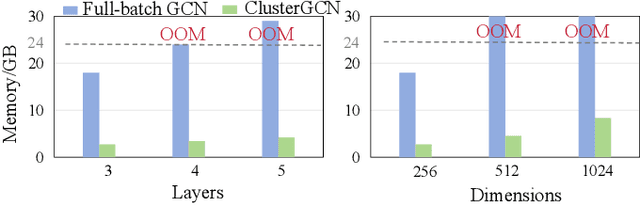
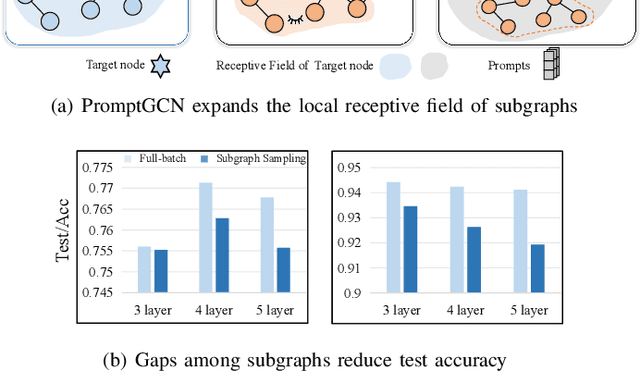
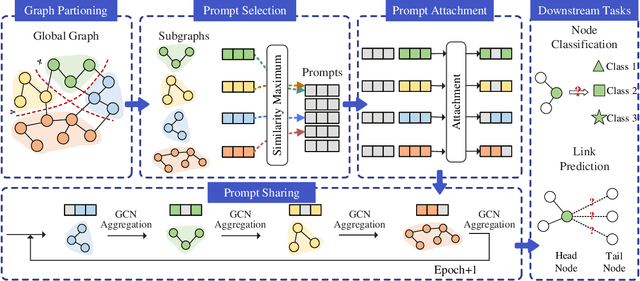
Graph Convolutional Networks (GCNs) are widely used in graph-based applications, such as social networks and recommendation systems. Nevertheless, large-scale graphs or deep aggregation layers in full-batch GCNs consume significant GPU memory, causing out of memory (OOM) errors on mainstream GPUs (e.g., 29GB memory consumption on the Ogbnproducts graph with 5 layers). The subgraph sampling methods reduce memory consumption to achieve lightweight GCNs by partitioning the graph into multiple subgraphs and sequentially training GCNs on each subgraph. However, these methods yield gaps among subgraphs, i.e., GCNs can only be trained based on subgraphs instead of global graph information, which reduces the accuracy of GCNs. In this paper, we propose PromptGCN, a novel prompt-based lightweight GCN model to bridge the gaps among subgraphs. First, the learnable prompt embeddings are designed to obtain global information. Then, the prompts are attached into each subgraph to transfer the global information among subgraphs. Extensive experimental results on seven largescale graphs demonstrate that PromptGCN exhibits superior performance compared to baselines. Notably, PromptGCN improves the accuracy of subgraph sampling methods by up to 5.48% on the Flickr dataset. Overall, PromptGCN can be easily combined with any subgraph sampling method to obtain a lightweight GCN model with higher accuracy.

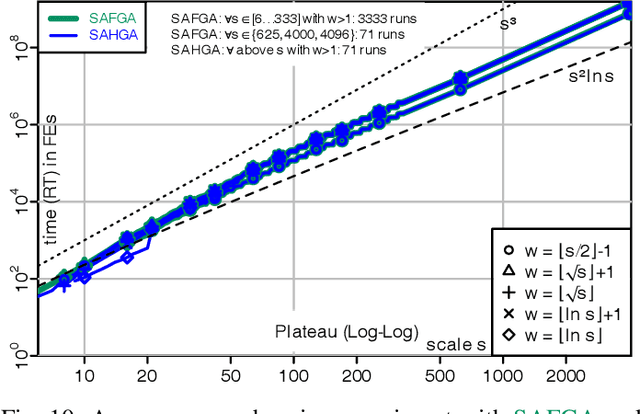
Frequency Fitness Assignment: Optimization without a Bias for Good Solutions can be Efficient

A fitness assignment process transforms the features (such as the objective value) of a candidate solution to a scalar fitness, which then is the basis for selection. Under Frequency Fitness Assignment (FFA), the fitness corresponding to an objective value is its encounter frequency and is subject to minimization. FFA creates algorithms that are not biased towards better solutions and are invariant under all bijections of the objective function value. We investigate the impact of FFA on the performance of two theory-inspired, state-of-the-art EAs, the Greedy (2+1) GA and the Self-Adjusting (1+(lambda,lambda)) GA. FFA improves their performance significantly on some problems that are hard for them. We empirically find that one FFA-based algorithm can solve all theory-based benchmark problems in this study, including traps, jumps, and plateaus, in polynomial time. We propose two hybrid approaches that use both direct and FFA-based optimization and find that they perform well. All FFA-based algorithms also perform better on satisfiability problems than all pure algorithm variants.

Frequency Fitness Assignment: Making Optimization Algorithms Invariant under Bijective Transformations of the Objective Function

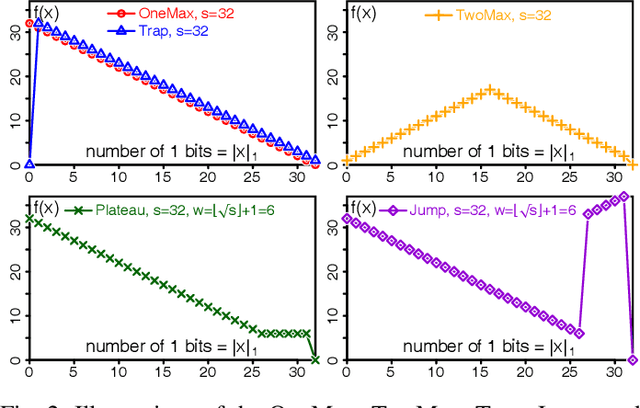
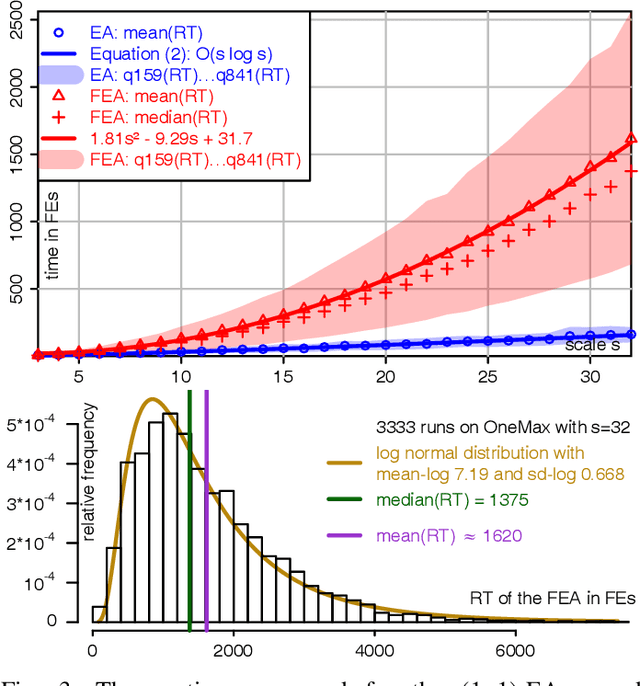
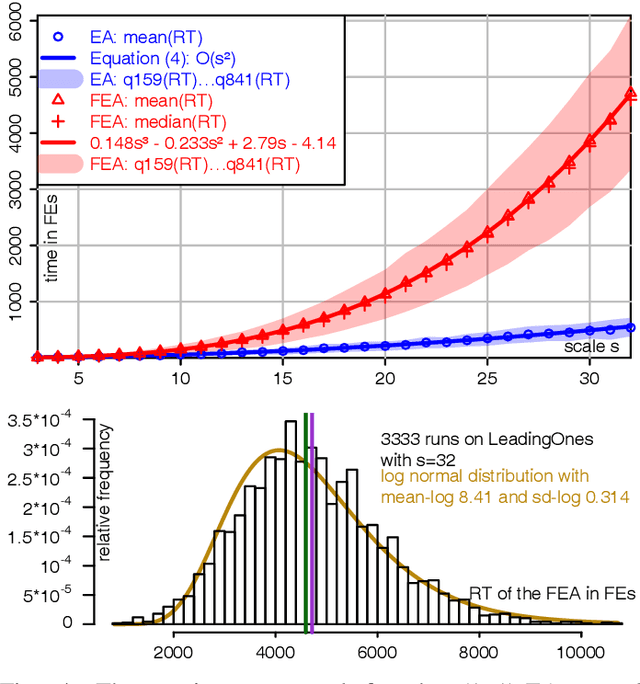
Under Frequency Fitness Assignment (FFA), the fitness corresponding to an objective value is its encounter frequency in fitness assignment steps and is subject to minimization. FFA renders optimization processes invariant under bijective transformations of the objective function. This is the strongest invariance property of any optimization procedure to our knowledge. On TwoMax, Jump, and Trap functions of scale s, a (1+1)-EA with standard mutation at rate 1/s can have expected running times exponential in s. In our experiments, a (1+1)-FEA, the same algorithm but using FFA, exhibits mean running times quadratic in s. Since Jump and Trap are bijective transformations of OneMax, it behaves identical on all three. On the LeadingOnes and Plateau problems, it seems to be slower than the (1+1)-EA by a factor linear in s. The (1+1)-FEA performs much better than the (1+1)-EA on W-Model and MaxSat instances. Due to the bijection invariance, the behavior of an optimization algorithm using FFA does not change when the objective values are encrypted. We verify this by applying the Md5 checksum computation as transformation to some of the above problems and yield the same behaviors. Finally, FFA can improve the performance of a Memetic Algorithm for Job Shop Scheduling.