Quantum computing and artificial intelligence: status and perspectives

This white paper discusses and explores the various points of intersection between quantum computing and artificial intelligence (AI). It describes how quantum computing could support the development of innovative AI solutions. It also examines use cases of classical AI that can empower research and development in quantum technologies, with a focus on quantum computing and quantum sensing. The purpose of this white paper is to provide a long-term research agenda aimed at addressing foundational questions about how AI and quantum computing interact and benefit one another. It concludes with a set of recommendations and challenges, including how to orchestrate the proposed theoretical work, align quantum AI developments with quantum hardware roadmaps, estimate both classical and quantum resources - especially with the goal of mitigating and optimizing energy consumption - advance this emerging hybrid software engineering discipline, and enhance European industrial competitiveness while considering societal implications.

Quantum Artificial Intelligence: A Brief Survey

Quantum Artificial Intelligence (QAI) is the intersection of quantum computing and AI, a technological synergy with expected significant benefits for both. In this paper, we provide a brief overview of what has been achieved in QAI so far and point to some open questions for future research. In particular, we summarize some major key findings on the feasability and the potential of using quantum computing for solving computationally hard problems in various subfields of AI, and vice versa, the leveraging of AI methods for building and operating quantum computing devices.

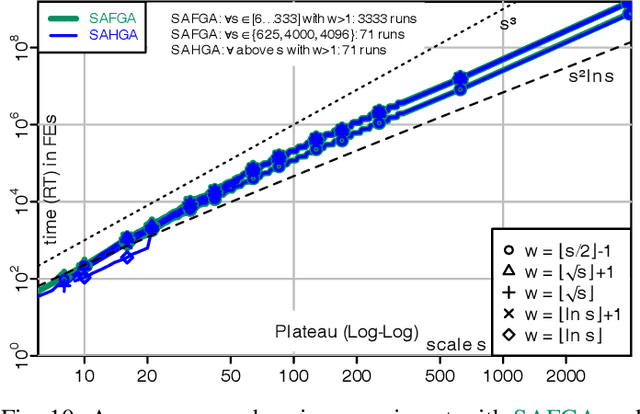
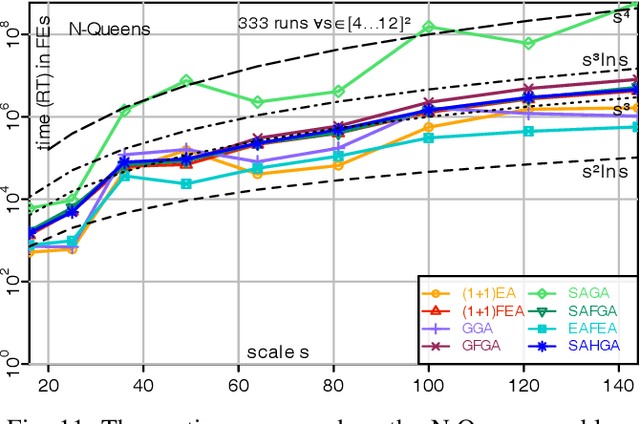
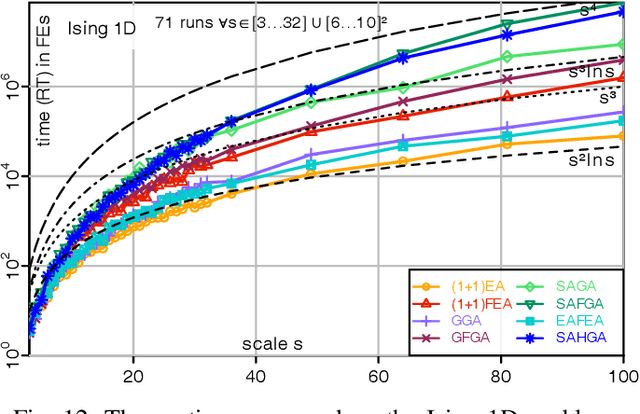
Frequency Fitness Assignment: Optimization without a Bias for Good Solutions can be Efficient

A fitness assignment process transforms the features (such as the objective value) of a candidate solution to a scalar fitness, which then is the basis for selection. Under Frequency Fitness Assignment (FFA), the fitness corresponding to an objective value is its encounter frequency and is subject to minimization. FFA creates algorithms that are not biased towards better solutions and are invariant under all bijections of the objective function value. We investigate the impact of FFA on the performance of two theory-inspired, state-of-the-art EAs, the Greedy (2+1) GA and the Self-Adjusting (1+(lambda,lambda)) GA. FFA improves their performance significantly on some problems that are hard for them. We empirically find that one FFA-based algorithm can solve all theory-based benchmark problems in this study, including traps, jumps, and plateaus, in polynomial time. We propose two hybrid approaches that use both direct and FFA-based optimization and find that they perform well. All FFA-based algorithms also perform better on satisfiability problems than all pure algorithm variants.

General Upper Bounds on the Running Time of Parallel Evolutionary Algorithms

We present a new method for analyzing the running time of parallel evolutionary algorithms with spatially structured populations. Based on the fitness-level method, it yields upper bounds on the expected parallel running time. This allows to rigorously estimate the speedup gained by parallelization. Tailored results are given for common migration topologies: ring graphs, torus graphs, hypercubes, and the complete graph. Example applications for pseudo-Boolean optimization show that our method is easy to apply and that it gives powerful results. In our examples the possible speedup increases with the density of the topology. Surprisingly, even sparse topologies like ring graphs lead to a significant speedup for many functions while not increasing the total number of function evaluations by more than a constant factor. We also identify which number of processors yield asymptotically optimal speedups, thus giving hints on how to parametrize parallel evolutionary algorithms.

Analysis of Speedups in Parallel Evolutionary Algorithms for Combinatorial Optimization

Evolutionary algorithms are popular heuristics for solving various combinatorial problems as they are easy to apply and often produce good results. Island models parallelize evolution by using different populations, called islands, which are connected by a graph structure as communication topology. Each island periodically communicates copies of good solutions to neighboring islands in a process called migration. We consider the speedup gained by island models in terms of the parallel running time for problems from combinatorial optimization: sorting (as maximization of sortedness), shortest paths, and Eulerian cycles. Different search operators are considered. The results show in which settings and up to what degree evolutionary algorithms can be parallelized efficiently. Along the way, we also investigate how island models deal with plateaus. In particular, we show that natural settings lead to exponential vs. logarithmic speedups, depending on the frequency of migration.