Frequency Fitness Assignment: Optimization without a Bias for Good Solutions can be Efficient

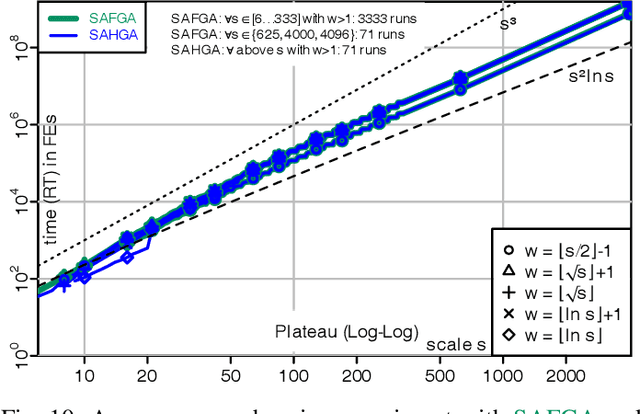
A fitness assignment process transforms the features (such as the objective value) of a candidate solution to a scalar fitness, which then is the basis for selection. Under Frequency Fitness Assignment (FFA), the fitness corresponding to an objective value is its encounter frequency and is subject to minimization. FFA creates algorithms that are not biased towards better solutions and are invariant under all bijections of the objective function value. We investigate the impact of FFA on the performance of two theory-inspired, state-of-the-art EAs, the Greedy (2+1) GA and the Self-Adjusting (1+(lambda,lambda)) GA. FFA improves their performance significantly on some problems that are hard for them. We empirically find that one FFA-based algorithm can solve all theory-based benchmark problems in this study, including traps, jumps, and plateaus, in polynomial time. We propose two hybrid approaches that use both direct and FFA-based optimization and find that they perform well. All FFA-based algorithms also perform better on satisfiability problems than all pure algorithm variants.