Frequency Fitness Assignment: Making Optimization Algorithms Invariant under Bijective Transformations of the Objective Function
Paper and Code
Jan 07, 2020
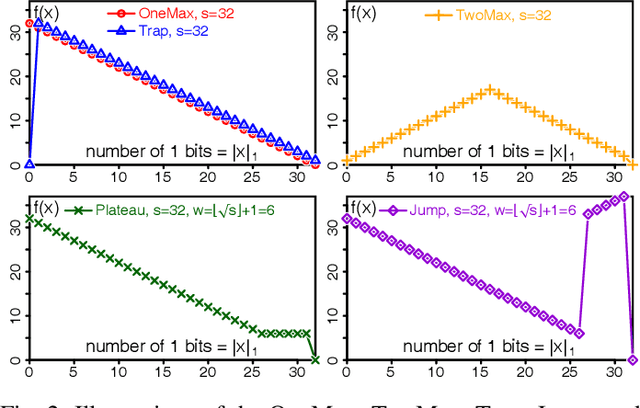
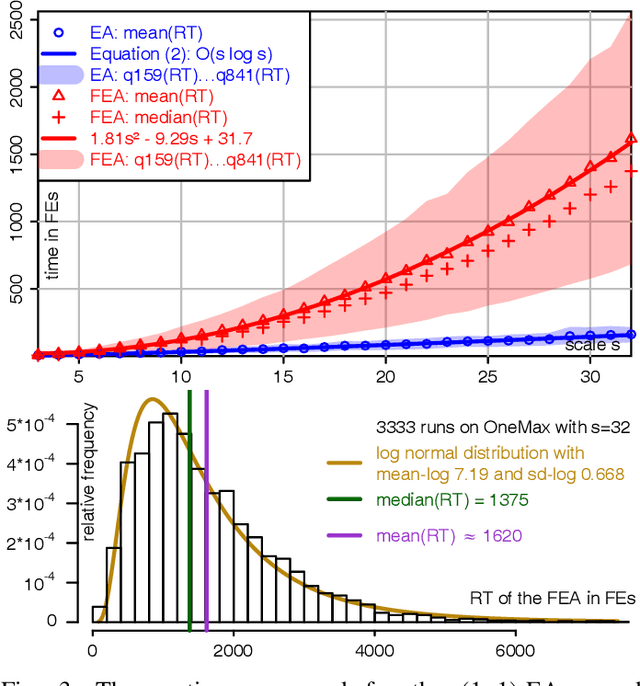
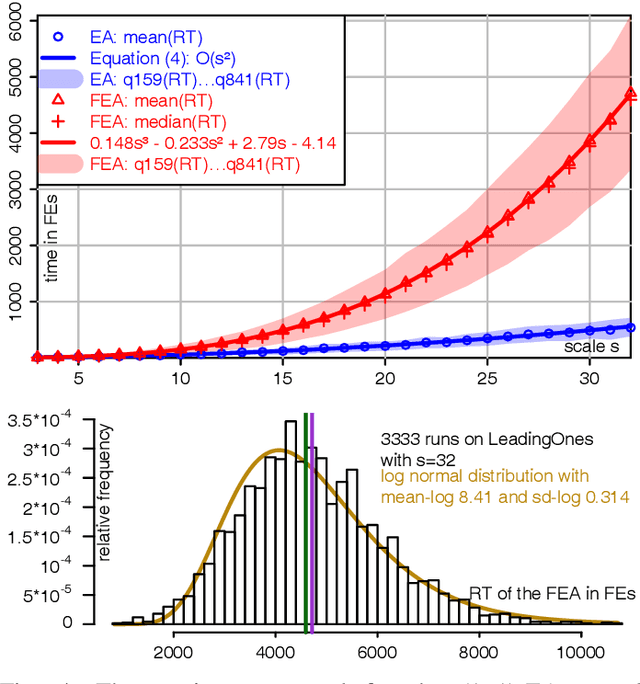
Under Frequency Fitness Assignment (FFA), the fitness corresponding to an objective value is its encounter frequency in fitness assignment steps and is subject to minimization. FFA renders optimization processes invariant under bijective transformations of the objective function. This is the strongest invariance property of any optimization procedure to our knowledge. On TwoMax, Jump, and Trap functions of scale s, a (1+1)-EA with standard mutation at rate 1/s can have expected running times exponential in s. In our experiments, a (1+1)-FEA, the same algorithm but using FFA, exhibits mean running times quadratic in s. Since Jump and Trap are bijective transformations of OneMax, it behaves identical on all three. On the LeadingOnes and Plateau problems, it seems to be slower than the (1+1)-EA by a factor linear in s. The (1+1)-FEA performs much better than the (1+1)-EA on W-Model and MaxSat instances. Due to the bijection invariance, the behavior of an optimization algorithm using FFA does not change when the objective values are encrypted. We verify this by applying the Md5 checksum computation as transformation to some of the above problems and yield the same behaviors. Finally, FFA can improve the performance of a Memetic Algorithm for Job Shop Scheduling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge