MAPS: Advancing Multi-Modal Reasoning in Expert-Level Physical Science

Pre-trained on extensive text and image corpora, current Multi-Modal Large Language Models (MLLM) have shown strong capabilities in general visual reasoning tasks. However, their performance is still lacking in physical domains that require understanding diagrams with complex physical structures and quantitative analysis based on multi-modal information. To address this, we develop a new framework, named Multi-Modal Scientific Reasoning with Physics Perception and Simulation (MAPS) based on an MLLM. MAPS decomposes expert-level multi-modal reasoning task into physical diagram understanding via a Physical Perception Model (PPM) and reasoning with physical knowledge via a simulator. The PPM module is obtained by fine-tuning a visual language model using carefully designed synthetic data with paired physical diagrams and corresponding simulation language descriptions. At the inference stage, MAPS integrates the simulation language description of the input diagram provided by PPM and results obtained through a Chain-of-Simulation process with MLLM to derive the underlying rationale and the final answer. Validated using our collected college-level circuit analysis problems, MAPS significantly improves reasoning accuracy of MLLM and outperforms all existing models. The results confirm MAPS offers a promising direction for enhancing multi-modal scientific reasoning ability of MLLMs. We will release our code, model and dataset used for our experiments upon publishing of this paper.

Improved Crowding Distance for NSGA-II

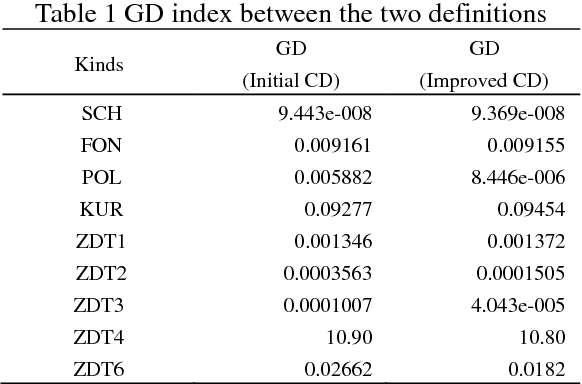
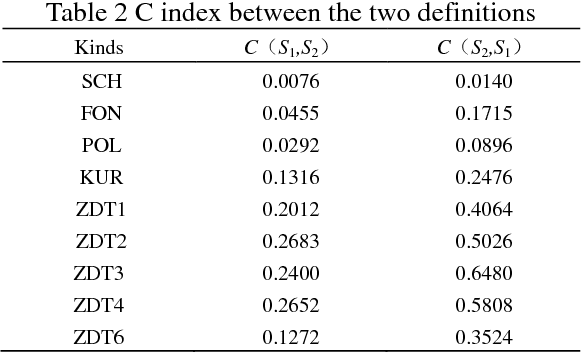
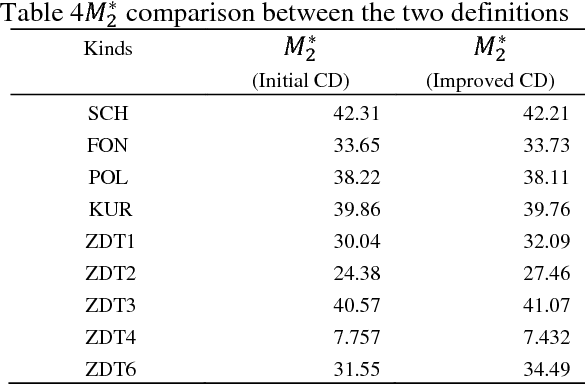
Non-dominated sorting genetic algorithm II (NSGA-II) does well in dealing with multi-objective problems. When evaluating validity of an algorithm for multi-objective problems, two kinds of indices are often considered simultaneously, i.e. the convergence to Pareto Front and the distribution characteristic. The crowding distance in the standard NSGA-II has the property that solutions within a cubic have the same crowding distance, which has no contribution to the convergence of the algorithm. Actually the closer to the Pareto Front a solution is, the higher priority it should have. In the paper, the crowding distance is redefined while keeping almost all the advantages of the original one. Moreover, the speed of converging to the Pareto Front is faster. Finally, the improvement is proved to be effective by applying it to solve nine Benchmark problems.