Adaptive KalmanNet: Data-Driven Kalman Filter with Fast Adaptation

Combining the classical Kalman filter (KF) with a deep neural network (DNN) enables tracking in partially known state space (SS) models. A major limitation of current DNN-aided designs stems from the need to train them to filter data originating from a specific distribution and underlying SS model. Consequently, changes in the model parameters may require lengthy retraining. While the KF adapts through parameter tuning, the black-box nature of DNNs makes identifying tunable components difficult. Hence, we propose Adaptive KalmanNet (AKNet), a DNN-aided KF that can adapt to changes in the SS model without retraining. Inspired by recent advances in large language model fine-tuning paradigms, AKNet uses a compact hypernetwork to generate context-dependent modulation weights. Numerical evaluation shows that AKNet provides consistent state estimation performance across a continuous range of noise distributions, even when trained using data from limited noise settings.

Unsupervised Learned Kalman Filtering

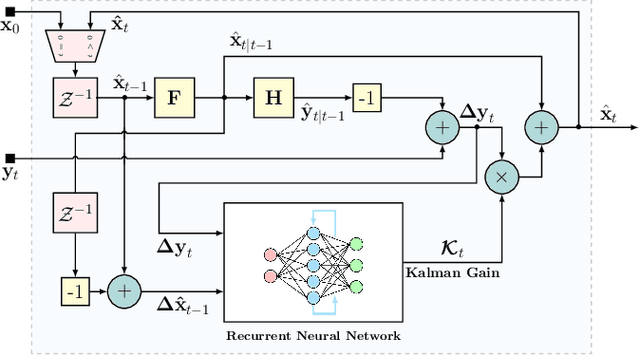
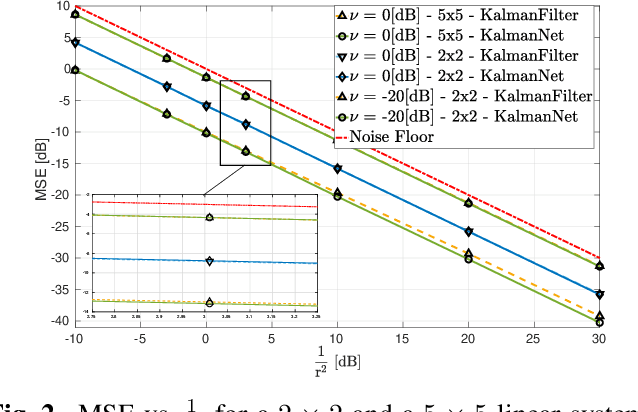
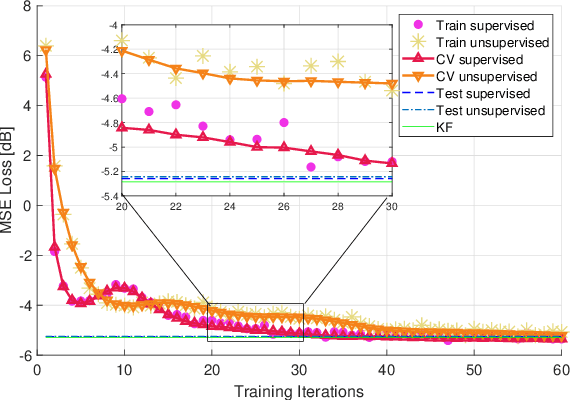
In this paper we adapt KalmanNet, which is a recently pro-posed deep neural network (DNN)-aided system whose architecture follows the operation of the model-based Kalman filter (KF), to learn its mapping in an unsupervised manner, i.e., without requiring ground-truth states. The unsupervised adaptation is achieved by exploiting the hybrid model-based/data-driven architecture of KalmanNet, which internally predicts the next observation as the KF does. These internal features are then used to compute the loss rather than the state estimate at the output of the system. With the capability of unsupervised learning, one can use KalmanNet not only to track the hidden state, but also to adapt to variations in the state space (SS) model. We numerically demonstrate that when the noise statistics are unknown, unsupervised KalmanNet achieves a similar performance to KalmanNet with supervised learning. We also show that we can adapt a pre-trained KalmanNet to changing SS models without providing additional data thanks to the unsupervised capabilities.

RTSNET: Deep Learning Aided Kalman Smoothing

The smoothing task is the core of many signal processing applications. It deals with the recovery of a sequence of hidden state variables from a sequence of noisy observations in a one-shot manner. In this work, we propose RTSNet, a highly efficient model-based, and data-driven smoothing algorithm. RTSNet integrates dedicated trainable models into the flow of the classical Rauch-Tung-Striebel (RTS) smoother and is able to outperform it when operating under model mismatch and non-linearities while retaining its efficiency and interoperability. Our numerical study demonstrates that althoughRTSNet is based on more compact neural networks, which leads to faster training and inference times, it outperforms the state-of-the-art data-driven smoother in a non-linear use case.

KalmanNet: Neural Network Aided Kalman Filtering for Partially Known Dynamics

Real-time state estimation of dynamical systems is a fundamental task in signal processing and control. For systems that are well-represented by a fully known linear Gaussian state space (SS) model, the celebrated Kalman filter (KF) is a low complexity optimal solution. However, both linearity of the underlying SS model and accurate knowledge of it are often not encountered in practice. Here, we present KalmanNet, a real-time state estimator that learns from data to carry out Kalman filtering under non-linear dynamics with partial information. By incorporating the structural SS model with a dedicated recurrent neural network module in the flow of the KF, we retain data efficiency and interpretability of the classic algorithm while implicitly learning complex dynamics from data. We numerically demonstrate that KalmanNet overcomes nonlinearities and model mismatch, outperforming classic filtering methods operating with both mismatched and accurate domain knowledge.