Xiaoye Jiang
Compressive Network Analysis
Apr 24, 2011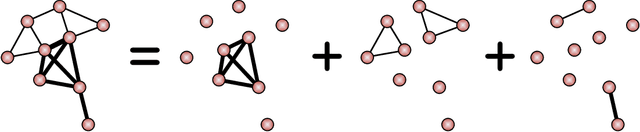
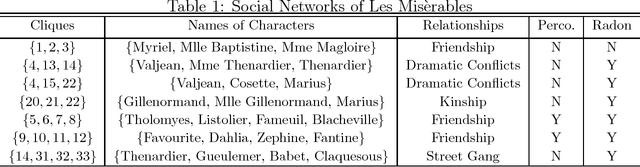
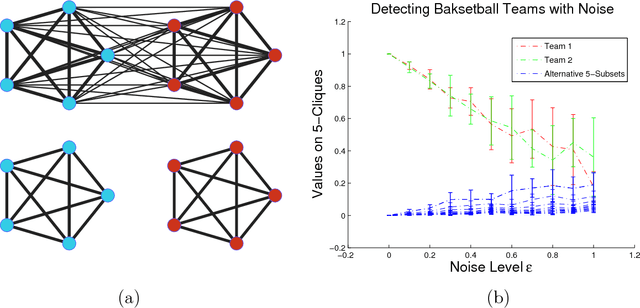
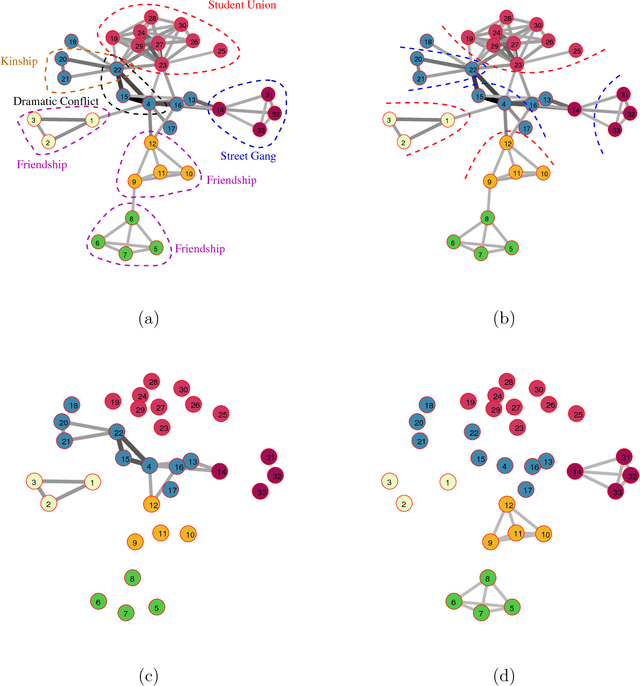
Abstract:Modern data acquisition routinely produces massive amounts of network data. Though many methods and models have been proposed to analyze such data, the research of network data is largely disconnected with the classical theory of statistical learning and signal processing. In this paper, we present a new framework for modeling network data, which connects two seemingly different areas: network data analysis and compressed sensing. From a nonparametric perspective, we model an observed network using a large dictionary. In particular, we consider the network clique detection problem and show connections between our formulation with a new algebraic tool, namely Randon basis pursuit in homogeneous spaces. Such a connection allows us to identify rigorous recovery conditions for clique detection problems. Though this paper is mainly conceptual, we also develop practical approximation algorithms for solving empirical problems and demonstrate their usefulness on real-world datasets.
Statistical ranking and combinatorial Hodge theory
Aug 10, 2009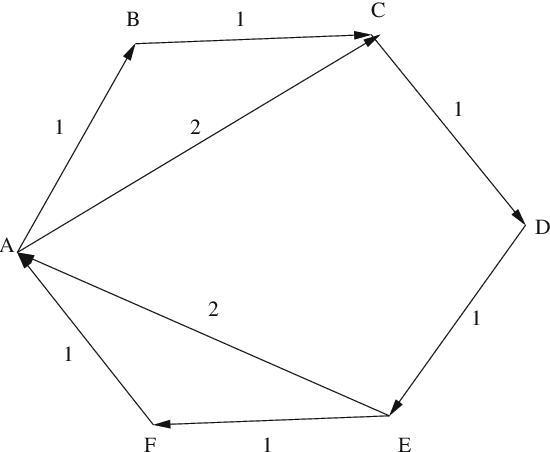
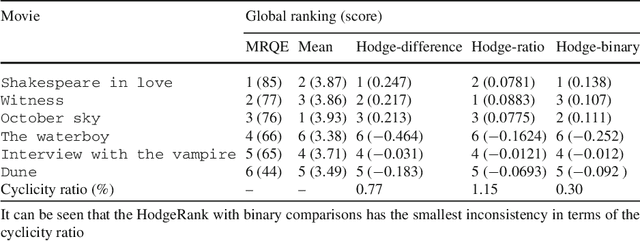
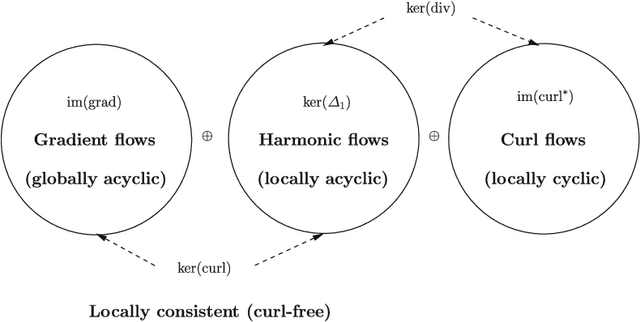
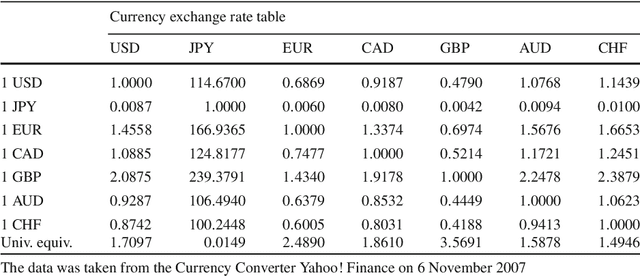
Abstract:We propose a number of techniques for obtaining a global ranking from data that may be incomplete and imbalanced -- characteristics almost universal to modern datasets coming from e-commerce and internet applications. We are primarily interested in score or rating-based cardinal data. From raw ranking data, we construct pairwise rankings, represented as edge flows on an appropriate graph. Our statistical ranking method uses the graph Helmholtzian, the graph theoretic analogue of the Helmholtz operator or vector Laplacian, in much the same way the graph Laplacian is an analogue of the Laplace operator or scalar Laplacian. We study the graph Helmholtzian using combinatorial Hodge theory: we show that every edge flow representing pairwise ranking can be resolved into two orthogonal components, a gradient flow that represents the L2-optimal global ranking and a divergence-free flow (cyclic) that measures the validity of the global ranking obtained -- if this is large, then the data does not have a meaningful global ranking. This divergence-free flow can be further decomposed orthogonally into a curl flow (locally cyclic) and a harmonic flow (locally acyclic but globally cyclic); these provides information on whether inconsistency arises locally or globally. An obvious advantage over the NP-hard Kemeny optimization is that discrete Hodge decomposition may be computed via a linear least squares regression. We also investigated the L1-projection of edge flows, showing that this is dual to correlation maximization over bounded divergence-free flows, and the L1-approximate sparse cyclic ranking, showing that this is dual to correlation maximization over bounded curl-free flows. We discuss relations with Kemeny optimization, Borda count, and Kendall-Smith consistency index from social choice theory and statistics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge