Convex Hull-based Algebraic Constraint for Visual Quadric SLAM

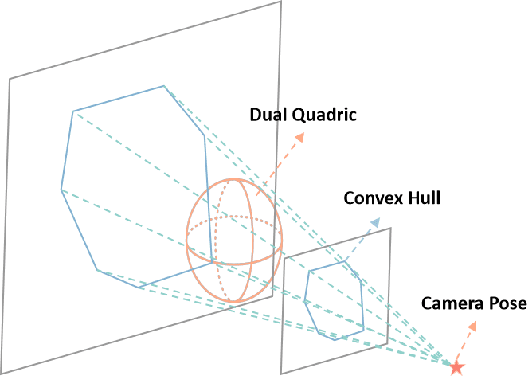
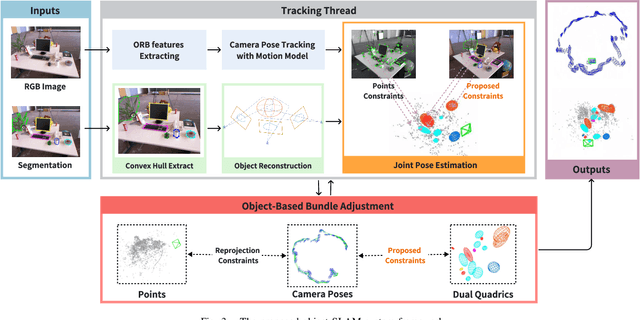
Using Quadrics as the object representation has the benefits of both generality and closed-form projection derivation between image and world spaces. Although numerous constraints have been proposed for dual quadric reconstruction, we found that many of them are imprecise and provide minimal improvements to localization.After scrutinizing the existing constraints, we introduce a concise yet more precise convex hull-based algebraic constraint for object landmarks, which is applied to object reconstruction, frontend pose estimation, and backend bundle adjustment.This constraint is designed to fully leverage precise semantic segmentation, effectively mitigating mismatches between complex-shaped object contours and dual quadrics.Experiments on public datasets demonstrate that our approach is applicable to both monocular and RGB-D SLAM and achieves improved object mapping and localization than existing quadric SLAM methods. The implementation of our method is available at https://github.com/tiev-tongji/convexhull-based-algebraic-constraint.

Dual sparse training framework: inducing activation map sparsity via Transformed $\ell1$ regularization

Although deep convolutional neural networks have achieved rapid development, it is challenging to widely promote and apply these models on low-power devices, due to computational and storage limitations. To address this issue, researchers have proposed techniques such as model compression, activation sparsity induction, and hardware accelerators. This paper presents a method to induce the sparsity of activation maps based on Transformed $\ell1$ regularization, so as to improve the research in the field of activation sparsity induction. Further, the method is innovatively combined with traditional pruning, constituting a dual sparse training framework. Compared to previous methods, Transformed $\ell1$ can achieve higher sparsity and better adapt to different network structures. Experimental results show that the method achieves improvements by more than 20\% in activation map sparsity on most models and corresponding datasets without compromising the accuracy. Specifically, it achieves a 27.52\% improvement for ResNet18 on the ImageNet dataset, and a 44.04\% improvement for LeNet5 on the MNIST dataset. In addition, the dual sparse training framework can greatly reduce the computational load and provide potential for reducing the required storage during runtime. Specifically, the ResNet18 and ResNet50 models obtained by the dual sparse training framework respectively reduce 81.7\% and 84.13\% of multiplicative floating-point operations, while maintaining accuracy and a low pruning rate.