Xiaoliang Song
Task Embedded Coordinate Update: A Realizable Framework for Multivariate Non-convex Optimization
Nov 05, 2018



Abstract:We in this paper propose a realizable framework TECU, which embeds task-specific strategies into update schemes of coordinate descent, for optimizing multivariate non-convex problems with coupled objective functions. On one hand, TECU is capable of improving algorithm efficiencies through embedding productive numerical algorithms, for optimizing univariate sub-problems with nice properties. From the other side, it also augments probabilities to receive desired results, by embedding advanced techniques in optimizations of realistic tasks. Integrating both numerical algorithms and advanced techniques together, TECU is proposed in a unified framework for solving a class of non-convex problems. Although the task embedded strategies bring inaccuracies in sub-problem optimizations, we provide a realizable criterion to control the errors, meanwhile, to ensure robust performances with rigid theoretical analyses. By respectively embedding ADMM and a residual-type CNN in our algorithm framework, the experimental results verify both efficiency and effectiveness of embedding task-oriented strategies in coordinate descent for solving practical problems.
An Optimization Framework with Flexible Inexact Inner Iterations for Nonconvex and Nonsmooth Programming
Jun 30, 2017


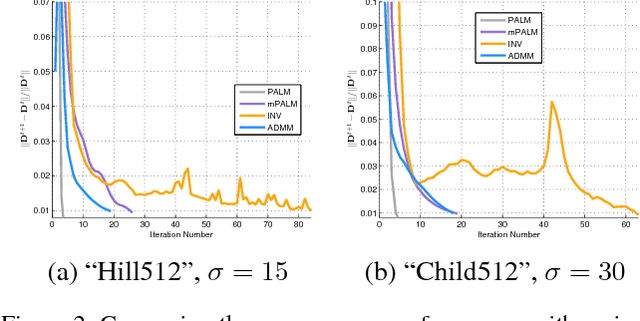
Abstract:In recent years, numerous vision and learning tasks have been (re)formulated as nonconvex and nonsmooth programmings(NNPs). Although some algorithms have been proposed for particular problems, designing fast and flexible optimization schemes with theoretical guarantee is a challenging task for general NNPs. It has been investigated that performing inexact inner iterations often benefit to special applications case by case, but their convergence behaviors are still unclear. Motivated by these practical experiences, this paper designs a novel algorithmic framework, named inexact proximal alternating direction method (IPAD) for solving general NNPs. We demonstrate that any numerical algorithms can be incorporated into IPAD for solving subproblems and the convergence of the resulting hybrid schemes can be consistently guaranteed by a series of simple error conditions. Beyond the guarantee in theory, numerical experiments on both synthesized and real-world data further demonstrate the superiority and flexibility of our IPAD framework for practical use.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge