FedFNN: Faster Training Convergence Through Update Predictions in Federated Recommender Systems

Federated Learning (FL) has emerged as a key approach for distributed machine learning, enhancing online personalization while ensuring user data privacy. Instead of sending private data to a central server as in traditional approaches, FL decentralizes computations: devices train locally and share updates with a global server. A primary challenge in this setting is achieving fast and accurate model training - vital for recommendation systems where delays can compromise user engagement. This paper introduces FedFNN, an algorithm that accelerates decentralized model training. In FL, only a subset of users are involved in each training epoch. FedFNN employs supervised learning to predict weight updates from unsampled users, using updates from the sampled set. Our evaluations, using real and synthetic data, show: 1. FedFNN achieves training speeds 5x faster than leading methods, maintaining or improving accuracy; 2. the algorithm's performance is consistent regardless of client cluster variations; 3. FedFNN outperforms other methods in scenarios with limited client availability, converging more quickly.

Projecting Markov Random Field Parameters for Fast Mixing

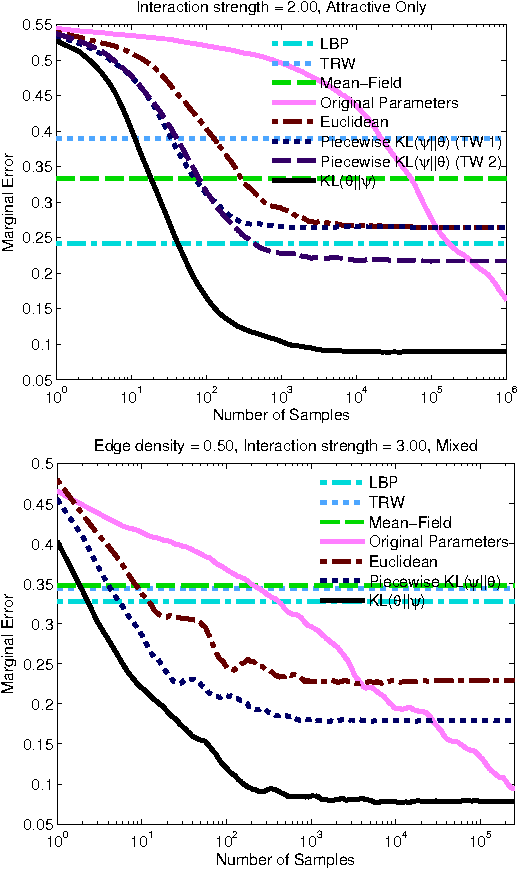
Markov chain Monte Carlo (MCMC) algorithms are simple and extremely powerful techniques to sample from almost arbitrary distributions. The flaw in practice is that it can take a large and/or unknown amount of time to converge to the stationary distribution. This paper gives sufficient conditions to guarantee that univariate Gibbs sampling on Markov Random Fields (MRFs) will be fast mixing, in a precise sense. Further, an algorithm is given to project onto this set of fast-mixing parameters in the Euclidean norm. Following recent work, we give an example use of this to project in various divergence measures, comparing univariate marginals obtained by sampling after projection to common variational methods and Gibbs sampling on the original parameters.

Projecting Ising Model Parameters for Fast Mixing

Inference in general Ising models is difficult, due to high treewidth making tree-based algorithms intractable. Moreover, when interactions are strong, Gibbs sampling may take exponential time to converge to the stationary distribution. We present an algorithm to project Ising model parameters onto a parameter set that is guaranteed to be fast mixing, under several divergences. We find that Gibbs sampling using the projected parameters is more accurate than with the original parameters when interaction strengths are strong and when limited time is available for sampling.