Projecting Markov Random Field Parameters for Fast Mixing
Paper and Code
Nov 12, 2014

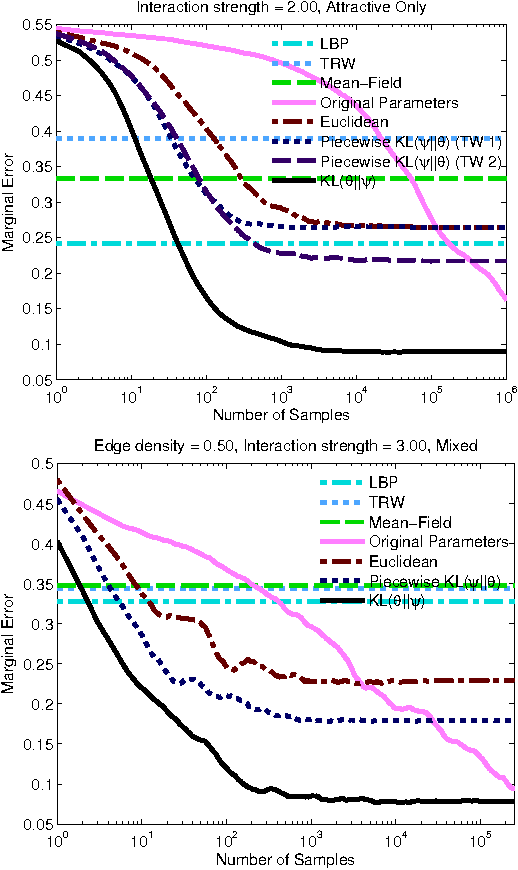

Markov chain Monte Carlo (MCMC) algorithms are simple and extremely powerful techniques to sample from almost arbitrary distributions. The flaw in practice is that it can take a large and/or unknown amount of time to converge to the stationary distribution. This paper gives sufficient conditions to guarantee that univariate Gibbs sampling on Markov Random Fields (MRFs) will be fast mixing, in a precise sense. Further, an algorithm is given to project onto this set of fast-mixing parameters in the Euclidean norm. Following recent work, we give an example use of this to project in various divergence measures, comparing univariate marginals obtained by sampling after projection to common variational methods and Gibbs sampling on the original parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge