Results of the 2024 CommonRoad Motion Planning Competition for Autonomous Vehicles

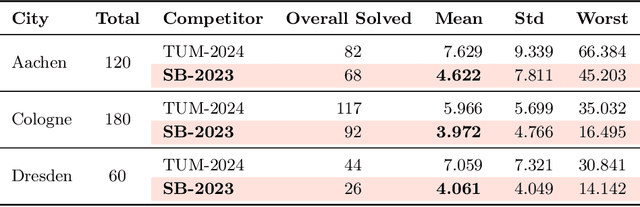
Over the past decade, a wide range of motion planning approaches for autonomous vehicles has been developed to handle increasingly complex traffic scenarios. However, these approaches are rarely compared on standardized benchmarks, limiting the assessment of relative strengths and weaknesses. To address this gap, we present the setup and results of the 4th CommonRoad Motion Planning Competition held in 2024, conducted using the CommonRoad benchmark suite. This annual competition provides an open-source and reproducible framework for benchmarking motion planning algorithms. The benchmark scenarios span highway and urban environments with diverse traffic participants, including passenger cars, buses, and bicycles. Planner performance is evaluated along four dimensions: efficiency, safety, comfort, and compliance with selected traffic rules. This report introduces the competition format and provides a comparison of representative high-performing planners from the 2023 and 2024 editions.

Understanding the Disharmony between Weight Normalization Family and Weight Decay: $ε-$shifted $L_2$ Regularizer

The merits of fast convergence and potentially better performance of the weight normalization family have drawn increasing attention in recent years. These methods use standardization or normalization that changes the weight $\boldsymbol{W}$ to $\boldsymbol{W}'$, which makes $\boldsymbol{W}'$ independent to the magnitude of $\boldsymbol{W}$. Surprisingly, $\boldsymbol{W}$ must be decayed during gradient descent, otherwise we will observe a severe under-fitting problem, which is very counter-intuitive since weight decay is widely known to prevent deep networks from over-fitting. In this paper, we \emph{theoretically} prove that the weight decay term $\frac{1}{2}\lambda||{\boldsymbol{W}}||^2$ merely modulates the effective learning rate for improving objective optimization, and has no influence on generalization when the weight normalization family is compositely employed. Furthermore, we also expose several critical problems when introducing weight decay term to weight normalization family, including the missing of global minimum and training instability. To address these problems, we propose an $\epsilon-$shifted $L_2$ regularizer, which shifts the $L_2$ objective by a positive constant $\epsilon$. Such a simple operation can theoretically guarantee the existence of global minimum, while preventing the network weights from being too small and thus avoiding gradient float overflow. It significantly improves the training stability and can achieve slightly better performance in our practice. The effectiveness of $\epsilon-$shifted $L_2$ regularizer is comprehensively validated on the ImageNet, CIFAR-100, and COCO datasets. Our codes and pretrained models will be released in https://github.com/implus/PytorchInsight.