Stochastic Hessian Fitting on Lie Group

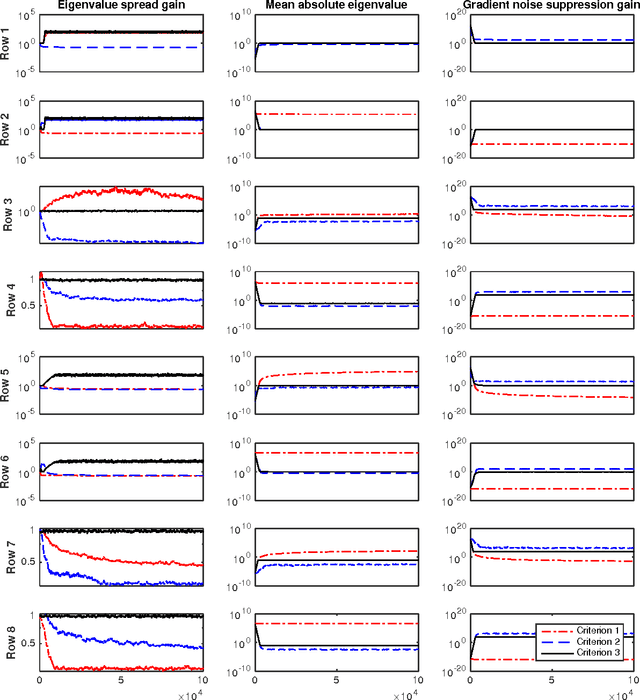
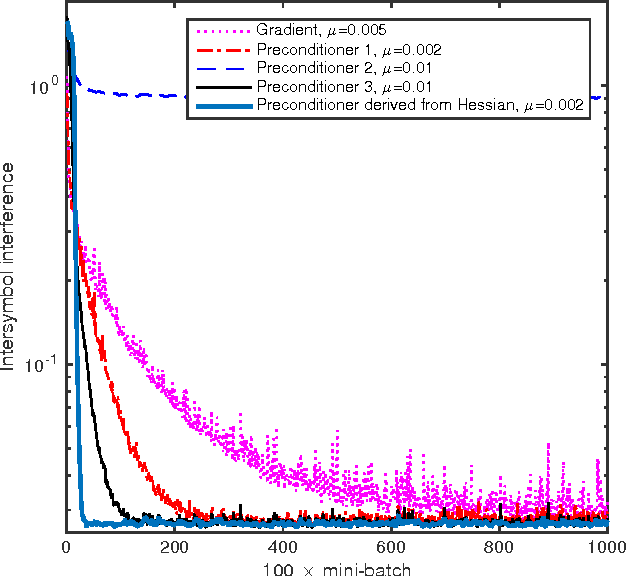
This paper studies the fitting of Hessian or its inverse with stochastic Hessian-vector products. A Hessian fitting criterion, which can be used to derive most of the commonly used methods, e.g., BFGS, Gaussian-Newton, AdaGrad, etc., is used for the analysis. Our studies reveal different convergence rates for different Hessian fitting methods, e.g., sublinear rates for gradient descent in the Euclidean space and a commonly used closed-form solution, linear rates for gradient descent on the manifold of symmetric positive definite (SPL) matrices and certain Lie groups. The Hessian fitting problem is further shown to be strongly convex under mild conditions on a specific yet general enough Lie group. To confirm our analysis, these methods are tested under different settings like noisy Hessian-vector products, time varying Hessians, and low precision arithmetic. These findings are useful for stochastic second order optimizations that rely on fast, robust and accurate Hessian estimations.

Curvature-Informed SGD via General Purpose Lie-Group Preconditioners

We present a novel approach to accelerate stochastic gradient descent (SGD) by utilizing curvature information obtained from Hessian-vector products or finite differences of parameters and gradients, similar to the BFGS algorithm. Our approach involves two preconditioners: a matrix-free preconditioner and a low-rank approximation preconditioner. We update both preconditioners online using a criterion that is robust to stochastic gradient noise and does not require line search or damping. To preserve the corresponding symmetry or invariance, our preconditioners are constrained to certain connected Lie groups. The Lie group's equivariance property simplifies the preconditioner fitting process, while its invariance property eliminates the need for damping, which is commonly required in second-order optimizers. As a result, the learning rate for parameter updating and the step size for preconditioner fitting are naturally normalized, and their default values work well in most scenarios. Our proposed approach offers a promising direction for improving the convergence of SGD with low computational overhead. We demonstrate that Preconditioned SGD (PSGD) outperforms SoTA on Vision, NLP, and RL tasks across multiple modern deep-learning architectures. We have provided code for reproducing toy and large scale experiments in this paper.

Multichannel Convolutive Speech Separation with Estimated Density Models

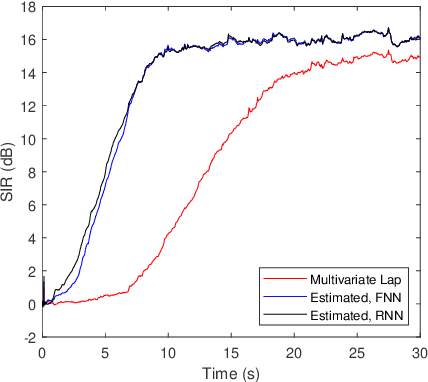
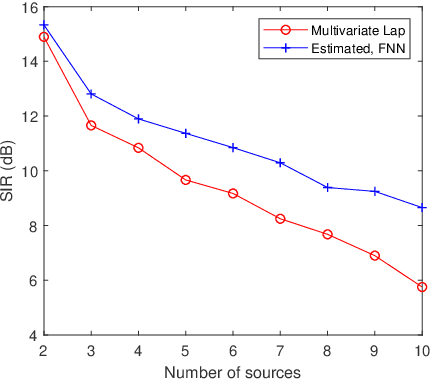
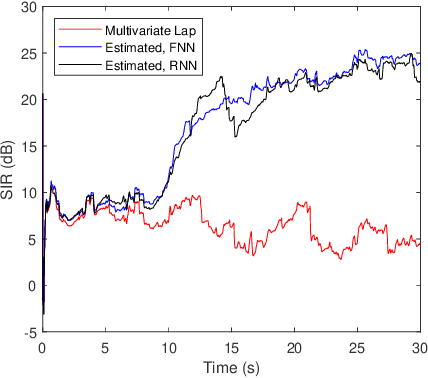
We consider the separation of convolutive speech mixtures in the framework of independent component analysis (ICA). Multivariate Laplace distribution is widely used for such tasks. But, it fails to capture the fine structures of speech signals, and limits the performance of separation. Here, we first time show that it is possible to efficiently learn the derivative of speech density with universal approximators like deep neural networks by optimizing certain proxy separation related performance indices. Specifically, we consider neural network density models for speech signals represented in the time-frequency domain, and compare them against the classic multivariate Laplace model for independent vector analysis (IVA). Experimental results suggest that the neural network density models significantly outperform multivariate Laplace one in tasks that require real time implementations, or involve the separation of a large number of speech sources.

A Triangular Network For Density Estimation

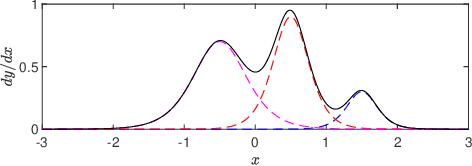
We report a triangular neural network implementation of neural autoregressive flow (NAF). Unlike many universal autoregressive density models, our design is highly modular, parameter economy, computationally efficient, and applicable to density estimation of data with high dimensions. It achieves state-of-the-art bits-per-dimension indices on MNIST and CIFAR-10 (about 1.1 and 3.7, respectively) in the category of general-purpose density estimators.

Learning with Labels of Existing and Nonexisting

We study the classification or detection problems where the label only suggests whether any instance of a class exists or does not exist in a training sample. No further information, e.g., the number of instances of each class, their locations or relative orders in the training data, is exploited. The model can be learned by maximizing the likelihood of the event that in a given training sample, instances of certain classes exist, while no instance of other classes exists. We use image recognition as the example task to develop our method, although it is applicable to data with higher or lower dimensions without much modification. Our method can be used to learn all convolutional neural networks for object detection and localization, e.g., reading street view house numbers in images with varying sizes, without using any further processing.

Learning Preconditioners on Lie Groups

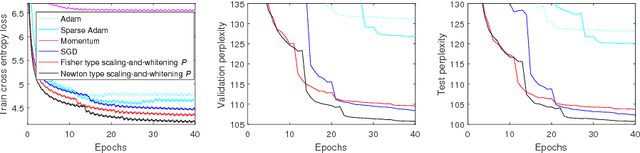
We study two types of preconditioners and preconditioned stochastic gradient descent (SGD) methods in a unified framework. We call the first one the Newton type due to its close relationship to Newton method, and the second one the Fisher type as its preconditioner is closely related to the inverse of Fisher information matrix. Both preconditioners can be derived from one framework, and efficiently learned on any matrix Lie groups designated by the user using natural or relative gradient descent. Many existing preconditioners and methods are special cases of either the Newton type or the Fisher type ones. Experimental results on relatively large scale machine learning problems are reported for performance study.

Online Second Order Methods for Non-Convex Stochastic Optimizations

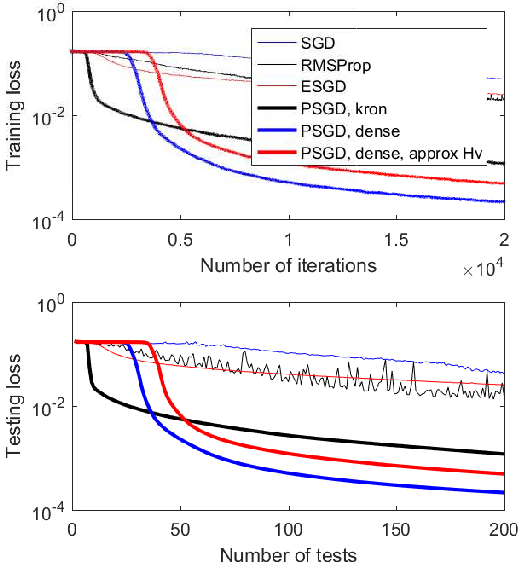
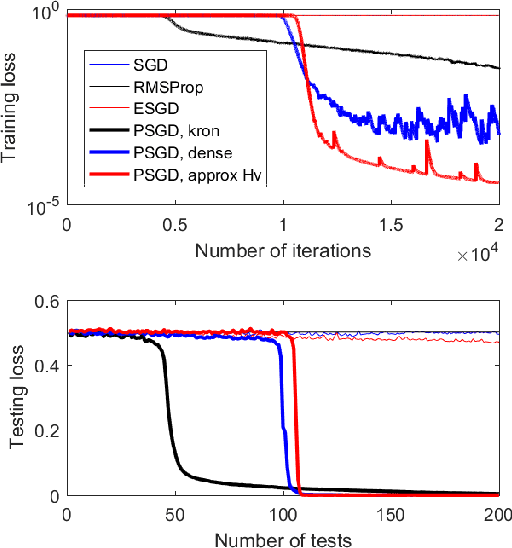
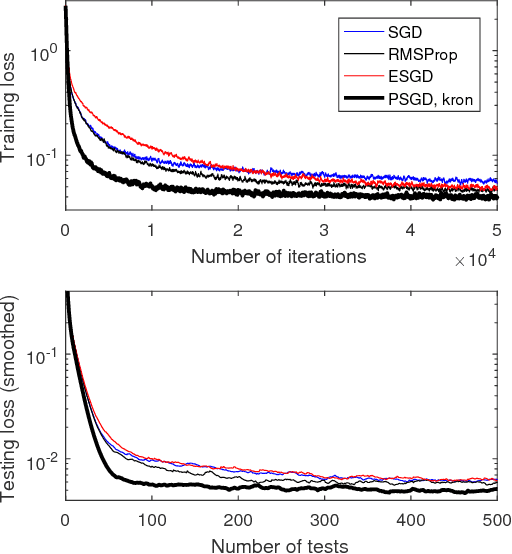
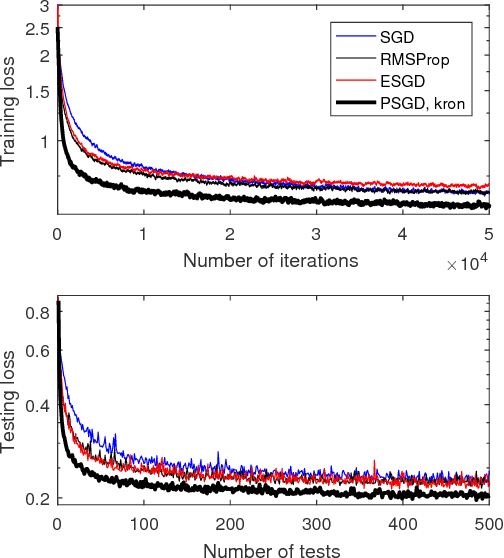
This paper proposes a family of online second order methods for possibly non-convex stochastic optimizations based on the theory of preconditioned stochastic gradient descent (PSGD), which can be regarded as an enhance stochastic Newton method with the ability to handle gradient noise and non-convexity simultaneously. We have improved the implementations of the original PSGD in several ways, e.g., new forms of preconditioners, more accurate Hessian vector product calculations, and better numerical stability with vanishing or ill-conditioned Hessian, etc.. We also have unrevealed the relationship between feature normalization and PSGD with Kronecker product preconditioners, which explains the excellent performance of Kronecker product preconditioners in deep neural network learning. A software package (https://github.com/lixilinx/psgd_tf) implemented in Tensorflow is provided to compare variations of stochastic gradient descent (SGD) and PSGD with five different preconditioners on a wide range of benchmark problems with commonly used neural network architectures, e.g., convolutional and recurrent neural networks. Experimental results clearly demonstrate the advantages of PSGD in terms of generalization performance and convergence speed.

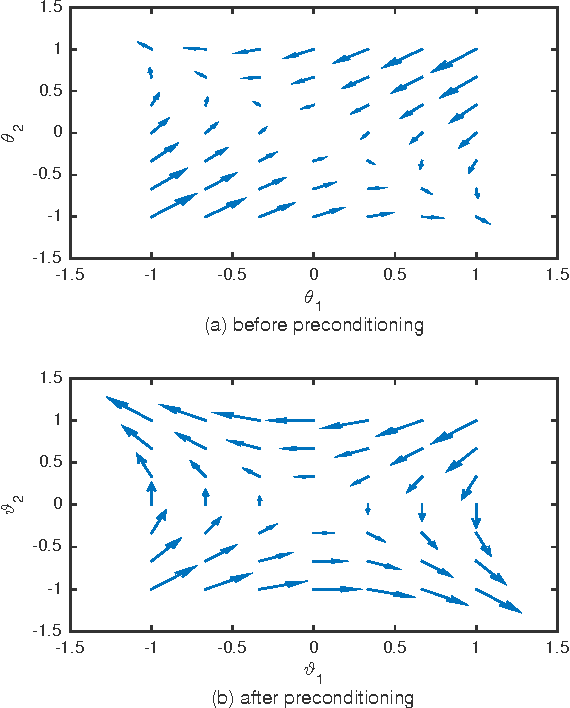
Preconditioned Stochastic Gradient Descent

Stochastic gradient descent (SGD) still is the workhorse for many practical problems. However, it converges slow, and can be difficult to tune. It is possible to precondition SGD to accelerate its convergence remarkably. But many attempts in this direction either aim at solving specialized problems, or result in significantly more complicated methods than SGD. This paper proposes a new method to estimate a preconditioner such that the amplitudes of perturbations of preconditioned stochastic gradient match that of the perturbations of parameters to be optimized in a way comparable to Newton method for deterministic optimization. Unlike the preconditioners based on secant equation fitting as done in deterministic quasi-Newton methods, which assume positive definite Hessian and approximate its inverse, the new preconditioner works equally well for both convex and non-convex optimizations with exact or noisy gradients. When stochastic gradient is used, it can naturally damp the gradient noise to stabilize SGD. Efficient preconditioner estimation methods are developed, and with reasonable simplifications, they are applicable to large scaled problems. Experimental results demonstrate that equipped with the new preconditioner, without any tuning effort, preconditioned SGD can efficiently solve many challenging problems like the training of a deep neural network or a recurrent neural network requiring extremely long term memories.

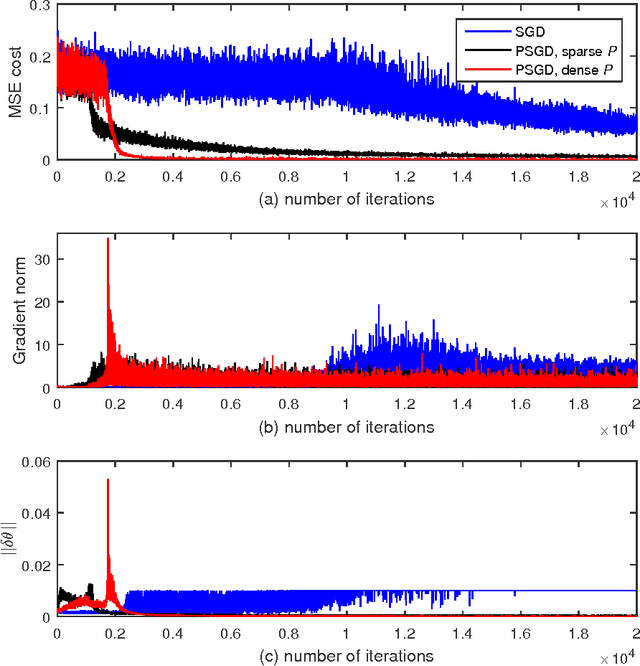
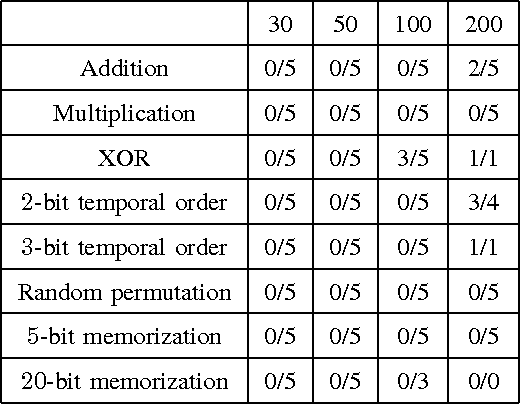
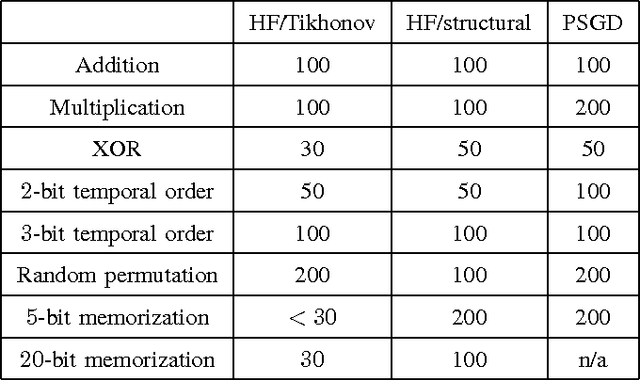
Recurrent neural network training with preconditioned stochastic gradient descent

This paper studies the performance of a recently proposed preconditioned stochastic gradient descent (PSGD) algorithm on recurrent neural network (RNN) training. PSGD adaptively estimates a preconditioner to accelerate gradient descent, and is designed to be simple, general and easy to use, as stochastic gradient descent (SGD). RNNs, especially the ones requiring extremely long term memories, are difficult to train. We have tested PSGD on a set of synthetic pathological RNN learning problems and the real world MNIST handwritten digit recognition task. Experimental results suggest that PSGD is able to achieve highly competitive performance without using any trick like preprocessing, pretraining or parameter tweaking.