Preconditioned Stochastic Gradient Descent
Paper and Code
Feb 22, 2017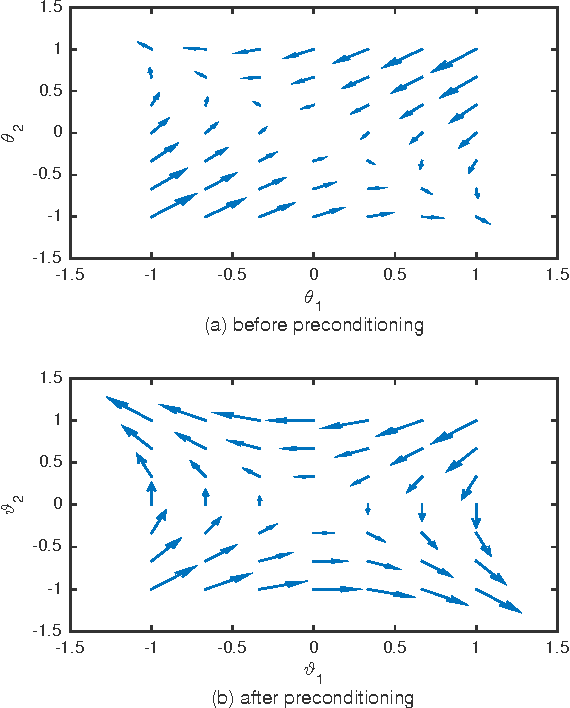
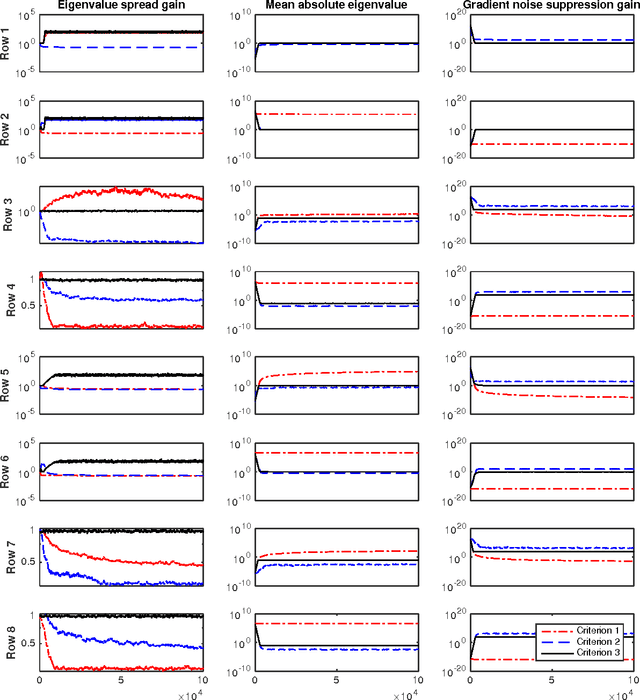
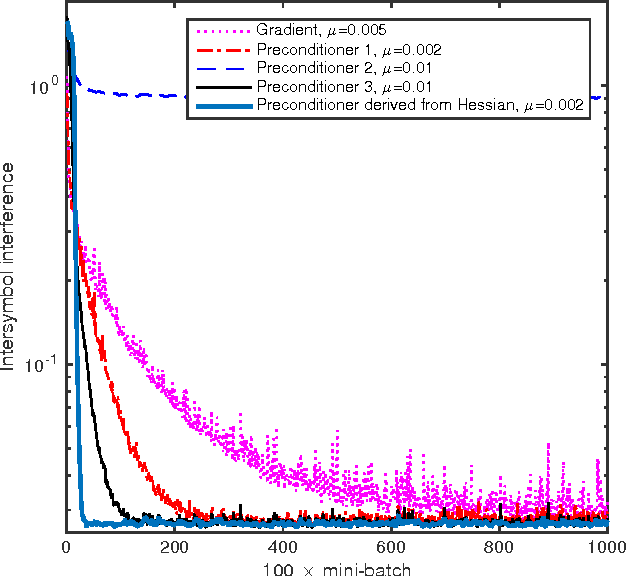

Stochastic gradient descent (SGD) still is the workhorse for many practical problems. However, it converges slow, and can be difficult to tune. It is possible to precondition SGD to accelerate its convergence remarkably. But many attempts in this direction either aim at solving specialized problems, or result in significantly more complicated methods than SGD. This paper proposes a new method to estimate a preconditioner such that the amplitudes of perturbations of preconditioned stochastic gradient match that of the perturbations of parameters to be optimized in a way comparable to Newton method for deterministic optimization. Unlike the preconditioners based on secant equation fitting as done in deterministic quasi-Newton methods, which assume positive definite Hessian and approximate its inverse, the new preconditioner works equally well for both convex and non-convex optimizations with exact or noisy gradients. When stochastic gradient is used, it can naturally damp the gradient noise to stabilize SGD. Efficient preconditioner estimation methods are developed, and with reasonable simplifications, they are applicable to large scaled problems. Experimental results demonstrate that equipped with the new preconditioner, without any tuning effort, preconditioned SGD can efficiently solve many challenging problems like the training of a deep neural network or a recurrent neural network requiring extremely long term memories.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge