Online Second Order Methods for Non-Convex Stochastic Optimizations
Paper and Code
Apr 29, 2018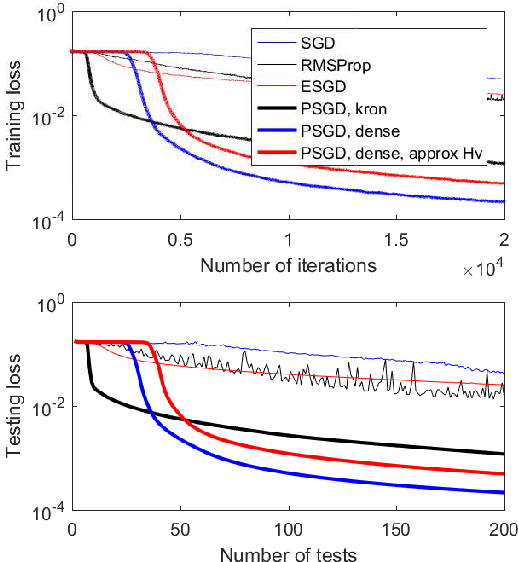
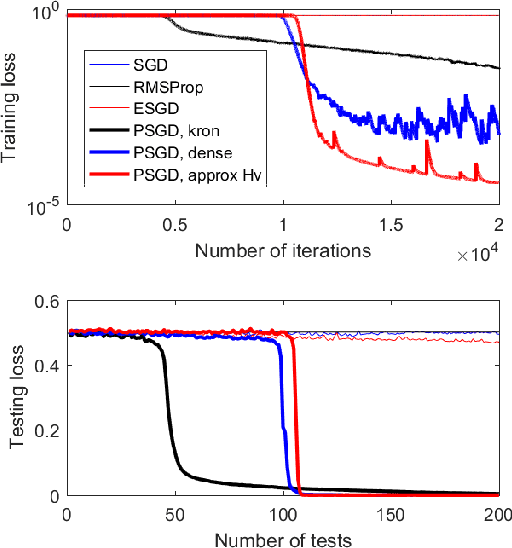
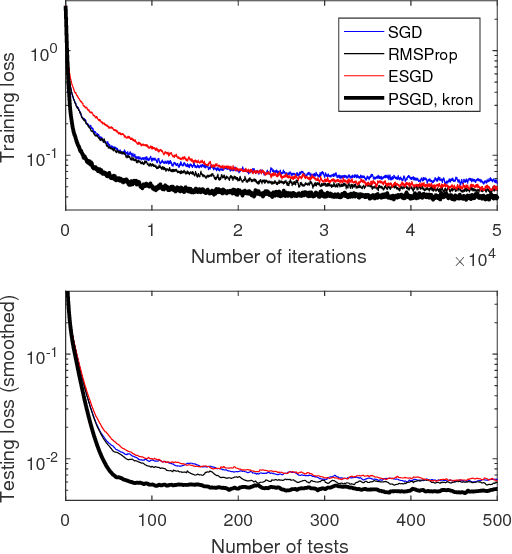
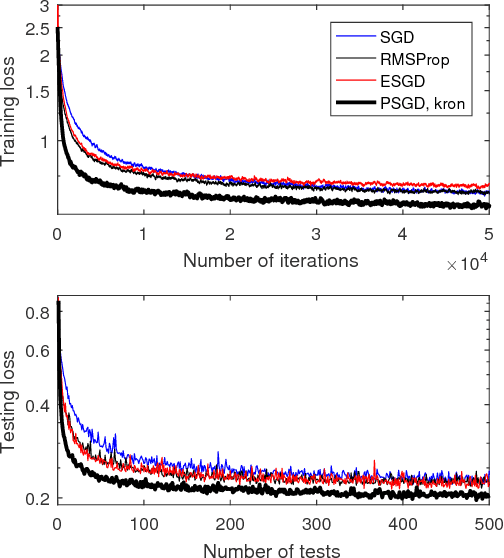
This paper proposes a family of online second order methods for possibly non-convex stochastic optimizations based on the theory of preconditioned stochastic gradient descent (PSGD), which can be regarded as an enhance stochastic Newton method with the ability to handle gradient noise and non-convexity simultaneously. We have improved the implementations of the original PSGD in several ways, e.g., new forms of preconditioners, more accurate Hessian vector product calculations, and better numerical stability with vanishing or ill-conditioned Hessian, etc.. We also have unrevealed the relationship between feature normalization and PSGD with Kronecker product preconditioners, which explains the excellent performance of Kronecker product preconditioners in deep neural network learning. A software package (https://github.com/lixilinx/psgd_tf) implemented in Tensorflow is provided to compare variations of stochastic gradient descent (SGD) and PSGD with five different preconditioners on a wide range of benchmark problems with commonly used neural network architectures, e.g., convolutional and recurrent neural networks. Experimental results clearly demonstrate the advantages of PSGD in terms of generalization performance and convergence speed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge