Multichannel Convolutive Speech Separation with Estimated Density Models

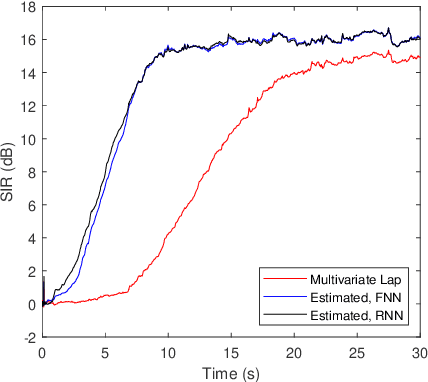
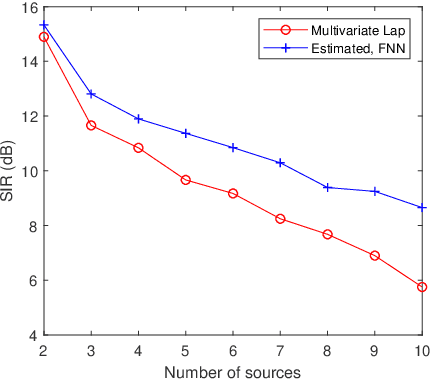
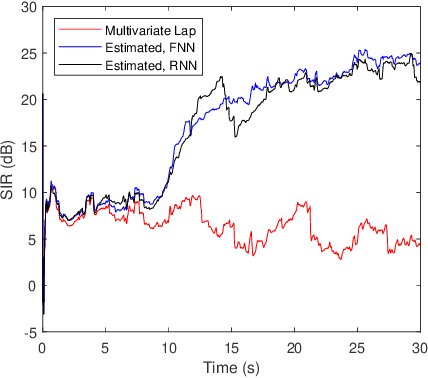
We consider the separation of convolutive speech mixtures in the framework of independent component analysis (ICA). Multivariate Laplace distribution is widely used for such tasks. But, it fails to capture the fine structures of speech signals, and limits the performance of separation. Here, we first time show that it is possible to efficiently learn the derivative of speech density with universal approximators like deep neural networks by optimizing certain proxy separation related performance indices. Specifically, we consider neural network density models for speech signals represented in the time-frequency domain, and compare them against the classic multivariate Laplace model for independent vector analysis (IVA). Experimental results suggest that the neural network density models significantly outperform multivariate Laplace one in tasks that require real time implementations, or involve the separation of a large number of speech sources.