Engineering software 2.0 by interpolating neural networks: unifying training, solving, and calibration

The evolution of artificial intelligence (AI) and neural network theories has revolutionized the way software is programmed, shifting from a hard-coded series of codes to a vast neural network. However, this transition in engineering software has faced challenges such as data scarcity, multi-modality of data, low model accuracy, and slow inference. Here, we propose a new network based on interpolation theories and tensor decomposition, the interpolating neural network (INN). Instead of interpolating training data, a common notion in computer science, INN interpolates interpolation points in the physical space whose coordinates and values are trainable. It can also extrapolate if the interpolation points reside outside of the range of training data and the interpolation functions have a larger support domain. INN features orders of magnitude fewer trainable parameters, faster training, a smaller memory footprint, and higher model accuracy compared to feed-forward neural networks (FFNN) or physics-informed neural networks (PINN). INN is poised to usher in Engineering Software 2.0, a unified neural network that spans various domains of space, time, parameters, and initial/boundary conditions. This has previously been computationally prohibitive due to the exponentially growing number of trainable parameters, easily exceeding the parameter size of ChatGPT, which is over 1 trillion. INN addresses this challenge by leveraging tensor decomposition and tensor product, with adaptable network architecture.

Statistical Parameterized Physics-Based Machine Learning Digital Twin Models for Laser Powder Bed Fusion Process

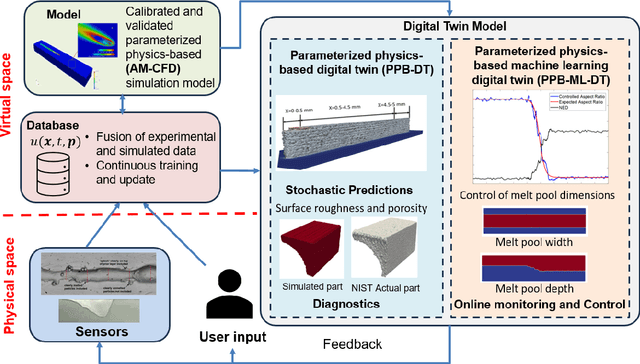
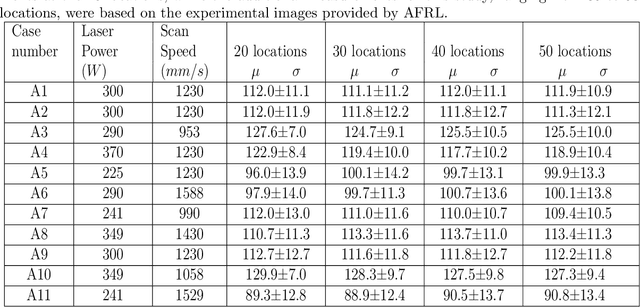
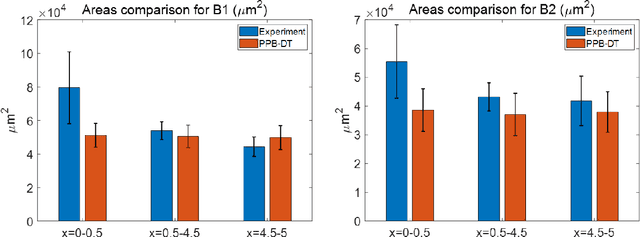
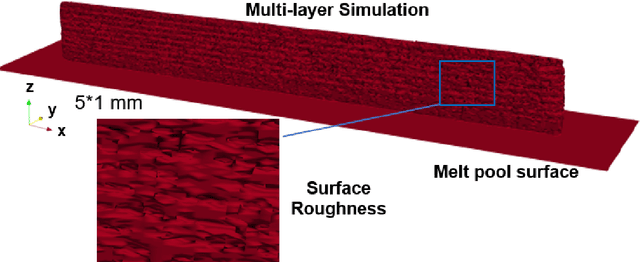
A digital twin (DT) is a virtual representation of physical process, products and/or systems that requires a high-fidelity computational model for continuous update through the integration of sensor data and user input. In the context of laser powder bed fusion (LPBF) additive manufacturing, a digital twin of the manufacturing process can offer predictions for the produced parts, diagnostics for manufacturing defects, as well as control capabilities. This paper introduces a parameterized physics-based digital twin (PPB-DT) for the statistical predictions of LPBF metal additive manufacturing process. We accomplish this by creating a high-fidelity computational model that accurately represents the melt pool phenomena and subsequently calibrating and validating it through controlled experiments. In PPB-DT, a mechanistic reduced-order method-driven stochastic calibration process is introduced, which enables the statistical predictions of the melt pool geometries and the identification of defects such as lack-of-fusion porosity and surface roughness, specifically for diagnostic applications. Leveraging data derived from this physics-based model and experiments, we have trained a machine learning-based digital twin (PPB-ML-DT) model for predicting, monitoring, and controlling melt pool geometries. These proposed digital twin models can be employed for predictions, control, optimization, and quality assurance within the LPBF process, ultimately expediting product development and certification in LPBF-based metal additive manufacturing.

An Introduction to Kernel and Operator Learning Methods for Homogenization by Self-consistent Clustering Analysis

Recent advances in operator learning theory have improved our knowledge about learning maps between infinite dimensional spaces. However, for large-scale engineering problems such as concurrent multiscale simulation for mechanical properties, the training cost for the current operator learning methods is very high. The article presents a thorough analysis on the mathematical underpinnings of the operator learning paradigm and proposes a kernel learning method that maps between function spaces. We first provide a survey of modern kernel and operator learning theory, as well as discuss recent results and open problems. From there, the article presents an algorithm to how we can analytically approximate the piecewise constant functions on R for operator learning. This implies the potential feasibility of success of neural operators on clustered functions. Finally, a k-means clustered domain on the basis of a mechanistic response is considered and the Lippmann-Schwinger equation for micro-mechanical homogenization is solved. The article briefly discusses the mathematics of previous kernel learning methods and some preliminary results with those methods. The proposed kernel operator learning method uses graph kernel networks to come up with a mechanistic reduced order method for multiscale homogenization.

HiDeNN-PGD: reduced-order hierarchical deep learning neural networks

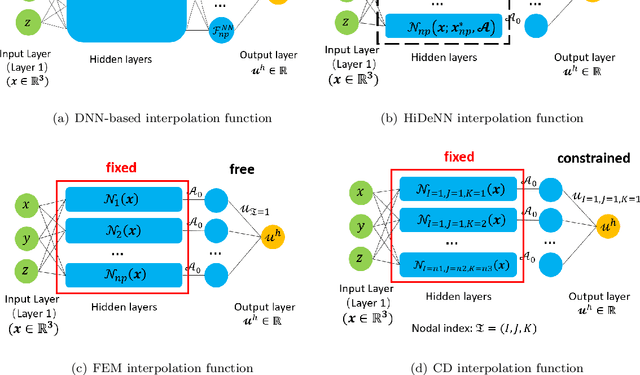
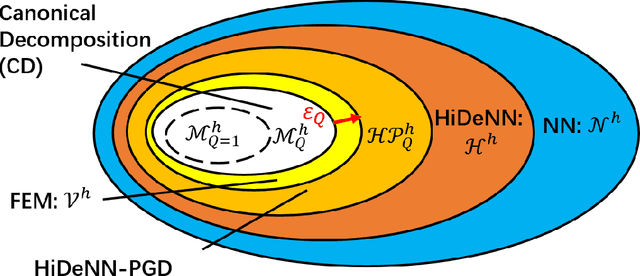
This paper presents a proper generalized decomposition (PGD) based reduced-order model of hierarchical deep-learning neural networks (HiDeNN). The proposed HiDeNN-PGD method keeps both advantages of HiDeNN and PGD methods. The automatic mesh adaptivity makes the HiDeNN-PGD more accurate than the finite element method (FEM) and conventional PGD, using a fraction of the FEM degrees of freedom. The accuracy and convergence of the method have been studied theoretically and numerically, with a comparison to different methods, including FEM, PGD, HiDeNN and Deep Neural Networks. In addition, we theoretically showed that the PGD converges to FEM at increasing modes, and the PGD error is a direct sum of the FEM error and the mode reduction error. The proposed HiDeNN-PGD performs high accuracy with orders of magnitude fewer degrees of freedom, which shows a high potential to achieve fast computations with a high level of accuracy for large-size engineering problems.