Single- to multi-fidelity history-dependent learning with uncertainty quantification and disentanglement: application to data-driven constitutive modeling

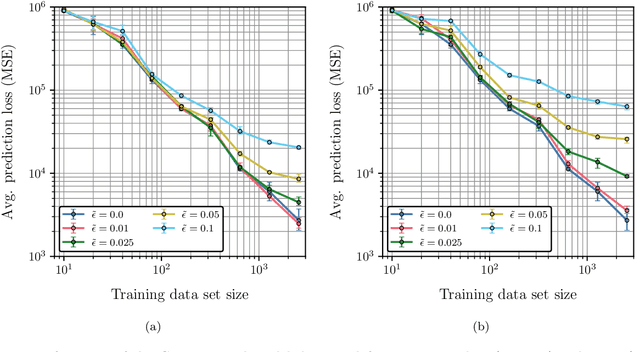
Data-driven learning is generalized to consider history-dependent multi-fidelity data, while quantifying epistemic uncertainty and disentangling it from data noise (aleatoric uncertainty). This generalization is hierarchical and adapts to different learning scenarios: from training the simplest single-fidelity deterministic neural networks up to the proposed multi-fidelity variance estimation Bayesian recurrent neural networks. The versatility and generality of the proposed methodology are demonstrated by applying it to different data-driven constitutive modeling scenarios that include multiple fidelities with and without aleatoric uncertainty (noise). The method accurately predicts the response and quantifies model error while also discovering the noise distribution (when present). This opens opportunities for future real-world applications in diverse scientific and engineering domains; especially, the most challenging cases involving design and analysis under uncertainty.

Automatically Differentiable Model Updating (ADiMU): conventional, hybrid, and neural network material model discovery including history-dependency

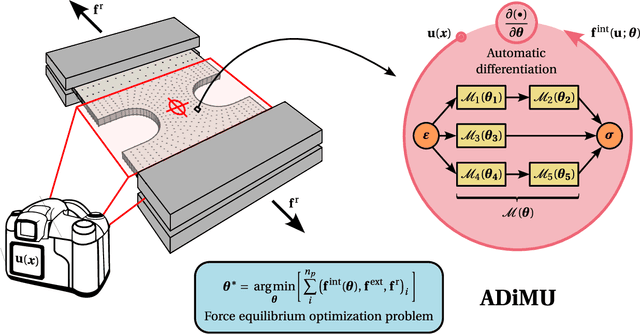
We introduce the first Automatically Differentiable Model Updating (ADiMU) framework that finds any history-dependent material model from full-field displacement and global force data (global, indirect discovery) or from strain-stress data (local, direct discovery). We show that ADiMU can update conventional (physics-based), neural network (data-driven), and hybrid material models. Moreover, this framework requires no fine-tuning of hyperparameters or additional quantities beyond those inherent to the user-selected material model architecture and optimizer. The robustness and versatility of ADiMU is extensively exemplified by updating different models spanning tens to millions of parameters, in both local and global discovery settings. Relying on fully differentiable code, the algorithmic implementation leverages vectorizing maps that enable history-dependent automatic differentiation via efficient batched execution of shared computation graphs. This contribution also aims to facilitate the integration, evaluation and application of future material model architectures by openly supporting the research community. Therefore, ADiMU is released as an open-source computational tool, integrated into a carefully designed and documented software named HookeAI.

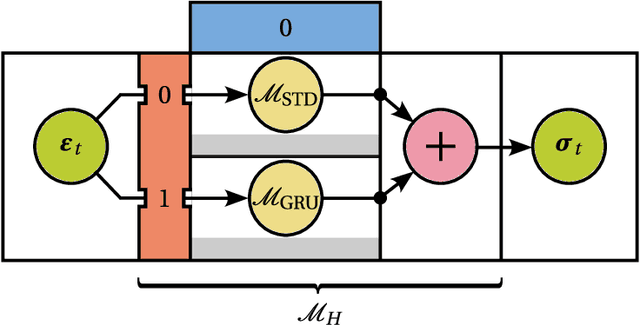
Cooperative Bayesian and variance networks disentangle aleatoric and epistemic uncertainties

Real-world data contains aleatoric uncertainty - irreducible noise arising from imperfect measurements or from incomplete knowledge about the data generation process. Mean variance estimation (MVE) networks can learn this type of uncertainty but require ad-hoc regularization strategies to avoid overfitting and are unable to predict epistemic uncertainty (model uncertainty). Conversely, Bayesian neural networks predict epistemic uncertainty but are notoriously difficult to train due to the approximate nature of Bayesian inference. We propose to cooperatively train a variance network with a Bayesian neural network and demonstrate that the resulting model disentangles aleatoric and epistemic uncertainties while improving the mean estimation. We demonstrate the effectiveness and scalability of this method across a diverse range of datasets, including a time-dependent heteroscedastic regression dataset we created where the aleatoric uncertainty is known. The proposed method is straightforward to implement, robust, and adaptable to various model architectures.

Consistent machine learning for topology optimization with microstructure-dependent neural network material models

Additive manufacturing methods together with topology optimization have enabled the creation of multiscale structures with controlled spatially-varying material microstructure. However, topology optimization or inverse design of such structures in the presence of nonlinearities remains a challenge due to the expense of computational homogenization methods and the complexity of differentiably parameterizing the microstructural response. A solution to this challenge lies in machine learning techniques that offer efficient, differentiable mappings between the material response and its microstructural descriptors. This work presents a framework for designing multiscale heterogeneous structures with spatially varying microstructures by merging a homogenization-based topology optimization strategy with a consistent machine learning approach grounded in hyperelasticity theory. We leverage neural architectures that adhere to critical physical principles such as polyconvexity, objectivity, material symmetry, and thermodynamic consistency to supply the framework with a reliable constitutive model that is dependent on material microstructural descriptors. Our findings highlight the potential of integrating consistent machine learning models with density-based topology optimization for enhancing design optimization of heterogeneous hyperelastic structures under finite deformations.

Practical multi-fidelity machine learning: fusion of deterministic and Bayesian models

Multi-fidelity machine learning methods address the accuracy-efficiency trade-off by integrating scarce, resource-intensive high-fidelity data with abundant but less accurate low-fidelity data. We propose a practical multi-fidelity strategy for problems spanning low- and high-dimensional domains, integrating a non-probabilistic regression model for the low-fidelity with a Bayesian model for the high-fidelity. The models are trained in a staggered scheme, where the low-fidelity model is transfer-learned to the high-fidelity data and a Bayesian model is trained for the residual. This three-model strategy -- deterministic low-fidelity, transfer learning, and Bayesian residual -- leads to a prediction that includes uncertainty quantification both for noisy and noiseless multi-fidelity data. The strategy is general and unifies the topic, highlighting the expressivity trade-off between the transfer-learning and Bayesian models (a complex transfer-learning model leads to a simpler Bayesian model, and vice versa). We propose modeling choices for two scenarios, and argue in favor of using a linear transfer-learning model that fuses 1) kernel ridge regression for low-fidelity with Gaussian processes for high-fidelity; or 2) deep neural network for low-fidelity with a Bayesian neural network for high-fidelity. We demonstrate the effectiveness and efficiency of the proposed strategies and contrast them with the state-of-the-art based on various numerical examples. The simplicity of these formulations makes them practical for a broad scope of future engineering applications.

Neural topology optimization: the good, the bad, and the ugly

Neural networks (NNs) hold great promise for advancing inverse design via topology optimization (TO), yet misconceptions about their application persist. This article focuses on neural topology optimization (neural TO), which leverages NNs to reparameterize the decision space and reshape the optimization landscape. While the method is still in its infancy, our analysis tools reveal critical insights into the NNs' impact on the optimization process. We demonstrate that the choice of NN architecture significantly influences the objective landscape and the optimizer's path to an optimum. Notably, NNs introduce non-convexities even in otherwise convex landscapes, potentially delaying convergence in convex problems but enhancing exploration for non-convex problems. This analysis lays the groundwork for future advancements by highlighting: 1) the potential of neural TO for non-convex problems and dedicated GPU hardware (the "good"), 2) the limitations in smooth landscapes (the "bad"), and 3) the complex challenge of selecting optimal NN architectures and hyperparameters for superior performance (the "ugly").

Engineering software 2.0 by interpolating neural networks: unifying training, solving, and calibration

The evolution of artificial intelligence (AI) and neural network theories has revolutionized the way software is programmed, shifting from a hard-coded series of codes to a vast neural network. However, this transition in engineering software has faced challenges such as data scarcity, multi-modality of data, low model accuracy, and slow inference. Here, we propose a new network based on interpolation theories and tensor decomposition, the interpolating neural network (INN). Instead of interpolating training data, a common notion in computer science, INN interpolates interpolation points in the physical space whose coordinates and values are trainable. It can also extrapolate if the interpolation points reside outside of the range of training data and the interpolation functions have a larger support domain. INN features orders of magnitude fewer trainable parameters, faster training, a smaller memory footprint, and higher model accuracy compared to feed-forward neural networks (FFNN) or physics-informed neural networks (PINN). INN is poised to usher in Engineering Software 2.0, a unified neural network that spans various domains of space, time, parameters, and initial/boundary conditions. This has previously been computationally prohibitive due to the exponentially growing number of trainable parameters, easily exceeding the parameter size of ChatGPT, which is over 1 trillion. INN addresses this challenge by leveraging tensor decomposition and tensor product, with adaptable network architecture.

Gradient-free neural topology optimization

Gradient-free optimizers allow for tackling problems regardless of the smoothness or differentiability of their objective function, but they require many more iterations to converge when compared to gradient-based algorithms. This has made them unviable for topology optimization due to the high computational cost per iteration and high dimensionality of these problems. We propose a pre-trained neural reparameterization strategy that leads to at least one order of magnitude decrease in iteration count when optimizing the designs in latent space, as opposed to the conventional approach without latent reparameterization. We demonstrate this via extensive computational experiments in- and out-of-distribution with the training data. Although gradient-based topology optimization is still more efficient for differentiable problems, such as compliance optimization of structures, we believe this work will open up a new path for problems where gradient information is not readily available (e.g. fracture).

Continual learning for surface defect segmentation by subnetwork creation and selection

We introduce a new continual (or lifelong) learning algorithm called LDA-CP&S that performs segmentation tasks without undergoing catastrophic forgetting. The method is applied to two different surface defect segmentation problems that are learned incrementally, i.e. providing data about one type of defect at a time, while still being capable of predicting every defect that was seen previously. Our method creates a defect-related subnetwork for each defect type via iterative pruning and trains a classifier based on linear discriminant analysis (LDA). At the inference stage, we first predict the defect type with LDA and then predict the surface defects using the selected subnetwork. We compare our method with other continual learning methods showing a significant improvement -- mean Intersection over Union better by a factor of two when compared to existing methods on both datasets. Importantly, our approach shows comparable results with joint training when all the training data (all defects) are seen simultaneously

iPINNs: Incremental learning for Physics-informed neural networks

Physics-informed neural networks (PINNs) have recently become a powerful tool for solving partial differential equations (PDEs). However, finding a set of neural network parameters that lead to fulfilling a PDE can be challenging and non-unique due to the complexity of the loss landscape that needs to be traversed. Although a variety of multi-task learning and transfer learning approaches have been proposed to overcome these issues, there is no incremental training procedure for PINNs that can effectively mitigate such training challenges. We propose incremental PINNs (iPINNs) that can learn multiple tasks (equations) sequentially without additional parameters for new tasks and improve performance for every equation in the sequence. Our approach learns multiple PDEs starting from the simplest one by creating its own subnetwork for each PDE and allowing each subnetwork to overlap with previously learned subnetworks. We demonstrate that previous subnetworks are a good initialization for a new equation if PDEs share similarities. We also show that iPINNs achieve lower prediction error than regular PINNs for two different scenarios: (1) learning a family of equations (e.g., 1-D convection PDE); and (2) learning PDEs resulting from a combination of processes (e.g., 1-D reaction-diffusion PDE). The ability to learn all problems with a single network together with learning more complex PDEs with better generalization than regular PINNs will open new avenues in this field.