Guiding adaptive shrinkage by co-data to improve regression-based prediction and feature selection

The high dimensional nature of genomics data complicates feature selection, in particular in low sample size studies - not uncommon in clinical prediction settings. It is widely recognized that complementary data on the features, `co-data', may improve results. Examples are prior feature groups or p-values from a related study. Such co-data are ubiquitous in genomics settings due to the availability of public repositories. Yet, the uptake of learning methods that structurally use such co-data is limited. We review guided adaptive shrinkage methods: a class of regression-based learners that use co-data to adapt the shrinkage parameters, crucial for the performance of those learners. We discuss technical aspects, but also the applicability in terms of types of co-data that can be handled. This class of methods is contrasted with several others. In particular, group-adaptive shrinkage is compared with the better-known sparse group-lasso by evaluating feature selection. Finally, we demonstrate the versatility of the guided shrinkage methodology by showing how to `do-it-yourself': we integrate implementations of a co-data learner and the spike-and-slab prior for the purpose of improving feature selection in genetics studies.

rags2ridges: A One-Stop-Shop for Graphical Modeling of High-Dimensional Precision Matrices

A graphical model is an undirected network representing the conditional independence properties between random variables. Graphical modeling has become part and parcel of systems or network approaches to multivariate data, in particular when the variable dimension exceeds the observation dimension. rags2ridges is an R package for graphical modeling of high-dimensional precision matrices. It provides a modular framework for the extraction, visualization, and analysis of Gaussian graphical models from high-dimensional data. Moreover, it can handle the incorporation of prior information as well as multiple heterogeneous data classes. As such, it provides a one-stop-shop for graphical modeling of high-dimensional precision matrices. The functionality of the package is illustrated with an example dataset pertaining to blood-based metabolite measurements in persons suffering from Alzheimer's Disease.

The Spectral Condition Number Plot for Regularization Parameter Determination

Many modern statistical applications ask for the estimation of a covariance (or precision) matrix in settings where the number of variables is larger than the number of observations. There exists a broad class of ridge-type estimators that employs regularization to cope with the subsequent singularity of the sample covariance matrix. These estimators depend on a penalty parameter and choosing its value can be hard, in terms of being computationally unfeasible or tenable only for a restricted set of ridge-type estimators. Here we introduce a simple graphical tool, the spectral condition number plot, for informed heuristic penalty parameter selection. The proposed tool is computationally friendly and can be employed for the full class of ridge-type covariance (precision) estimators.

Targeted Fused Ridge Estimation of Inverse Covariance Matrices from Multiple High-Dimensional Data Classes

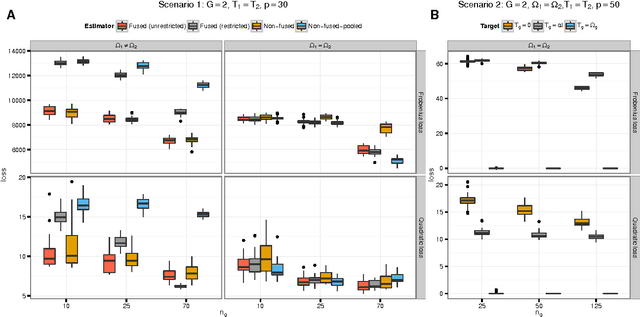
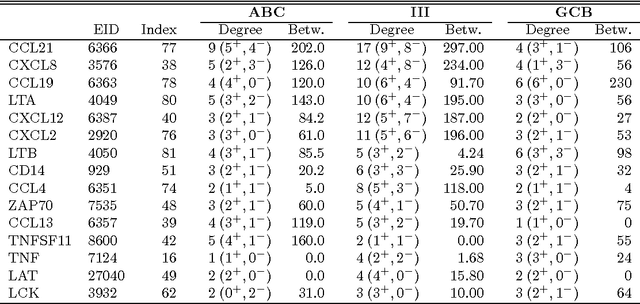
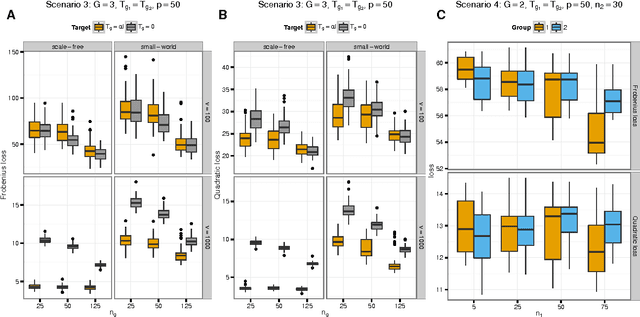
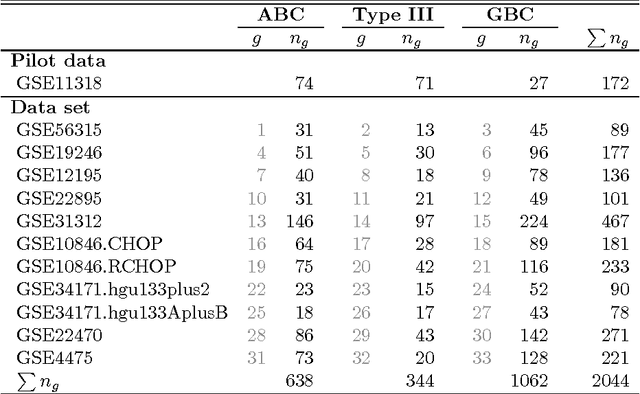
We consider the problem of jointly estimating multiple precision matrices from (aggregated) high-dimensional data consisting of distinct classes. An $\ell_2$-penalized maximum-likelihood approach is employed. The suggested approach is flexible and generic, incorporating several other $\ell_2$-penalized estimators as special cases. In addition, the approach allows for the specification of target matrices through which prior knowledge may be incorporated and which can stabilize the estimation procedure in high-dimensional settings. The result is a targeted fused ridge estimator that is of use when the precision matrices of the constituent classes are believed to chiefly share the same structure while potentially differing in a number of locations of interest. It has many applications in (multi)factorial study designs. We focus on the graphical interpretation of precision matrices with the proposed estimator then serving as a basis for integrative or meta-analytic Gaussian graphical modeling. Situations are considered in which the classes are defined by data sets and/or (subtypes of) diseases. The performance of the proposed estimator in the graphical modeling setting is assessed through extensive simulation experiments. Its practical usability is illustrated by the differential network modeling of 11 large-scale diffuse large B-cell lymphoma gene expression data sets. The estimator and its related procedures are incorporated into the R-package rags2ridges.