Introduction to dynamical mean-field theory of generic random neural networks

Dynamical mean-field theory is a powerful physics tool used to analyze the typical behavior of neural networks, where neurons can be recurrently connected, or multiple layers of neurons can be stacked. However, it is not easy for beginners to access the essence of this tool and the underlying physics. Here, we give a pedagogical introduction of this method in a particular example of generic random neural networks, where neurons are randomly and fully connected by correlated synapses and therefore the network exhibits rich emergent collective dynamics. We also review related past and recent important works applying this tool. In addition, a physically transparent and alternative method, namely the dynamical cavity method, is also introduced to derive exactly the same results. The numerical implementation of solving the integro-differential mean-field equations is also detailed, with an illustration of exploring the fluctuation dissipation theorem.

Statistical mechanics of continual learning: variational principle and mean-field potential

An obstacle to artificial general intelligence is set by the continual learning of multiple tasks of different nature. Recently, various heuristic tricks, both from machine learning and from neuroscience angles, were proposed, but they lack a unified theory ground. Here, we focus on the continual learning in single-layered and multi-layered neural networks of binary weights. A variational Bayesian learning setting is thus proposed, where the neural network is trained in a field-space, rather than the gradient-ill-defined discrete-weight space, and furthermore, the weight uncertainty is naturally incorporated, and modulates the synaptic resources among tasks. From a physics perspective, we translate the variational continual learning into the Franz-Parisi thermodynamic potential framework, where the previous task knowledge acts as a prior and a reference as well. Therefore, the learning performance can be analytically studied with mean-field order parameters, whose predictions coincide with the numerical experiments using stochastic gradient descent methods. Our proposed principled frameworks also connect to elastic weight consolidation, and neuroscience inspired metaplasticity, providing a theory-grounded method for the real-world multi-task learning with deep networks.

Graph Flow: Cross-layer Graph Flow Distillation for Dual Efficient Medical Image Segmentation

With the development of deep convolutional neural networks, medical image segmentation has achieved a series of breakthroughs in recent years. However, the higher-performance convolutional neural networks always mean numerous parameters and high computation costs, which will hinder the applications in clinical scenarios. Meanwhile, the scarceness of large-scale annotated medical image datasets further impedes the application of high-performance networks. To tackle these problems, we propose Graph Flow, a comprehensive knowledge distillation framework, for both network-efficiency and annotation-efficiency medical image segmentation. Specifically, our core Graph Flow Distillation transfer the essence of cross-layer variations from a well-trained cumbersome teacher network to a non-trained compact student network. In addition, an unsupervised Paraphraser Module is designed to purify the knowledge of the teacher network, which is also beneficial for the stabilization of training procedure. Furthermore, we build a unified distillation framework by integrating the adversarial distillation and the vanilla logits distillation, which can further refine the final predictions of the compact network. Extensive experiments conducted on Gastric Cancer Segmentation Dataset and Synapse Multi-organ Segmentation Dataset demonstrate the prominent ability of our method which achieves state-of-the-art performance on these different-modality and multi-category medical image datasets. Moreover, we demonstrate the effectiveness of our Graph Flow through a new semi-supervised paradigm for dual efficient medical image segmentation. Our code will be available at Graph Flow.

CoCo DistillNet: a Cross-layer Correlation Distillation Network for Pathological Gastric Cancer Segmentation

In recent years, deep convolutional neural networks have made significant advances in pathology image segmentation. However, pathology image segmentation encounters with a dilemma in which the higher-performance networks generally require more computational resources and storage. This phenomenon limits the employment of high-accuracy networks in real scenes due to the inherent high-resolution of pathological images. To tackle this problem, we propose CoCo DistillNet, a novel Cross-layer Correlation (CoCo) knowledge distillation network for pathological gastric cancer segmentation. Knowledge distillation, a general technique which aims at improving the performance of a compact network through knowledge transfer from a cumbersome network. Concretely, our CoCo DistillNet models the correlations of channel-mixed spatial similarity between different layers and then transfers this knowledge from a pre-trained cumbersome teacher network to a non-trained compact student network. In addition, we also utilize the adversarial learning strategy to further prompt the distilling procedure which is called Adversarial Distillation (AD). Furthermore, to stabilize our training procedure, we make the use of the unsupervised Paraphraser Module (PM) to boost the knowledge paraphrase in the teacher network. As a result, extensive experiments conducted on the Gastric Cancer Segmentation Dataset demonstrate the prominent ability of CoCo DistillNet which achieves state-of-the-art performance.

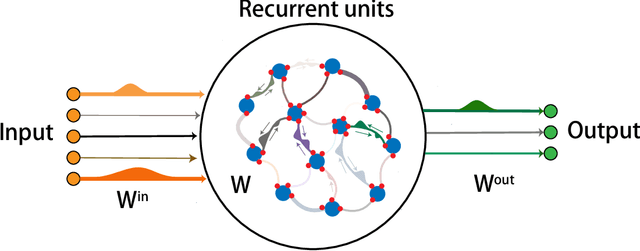
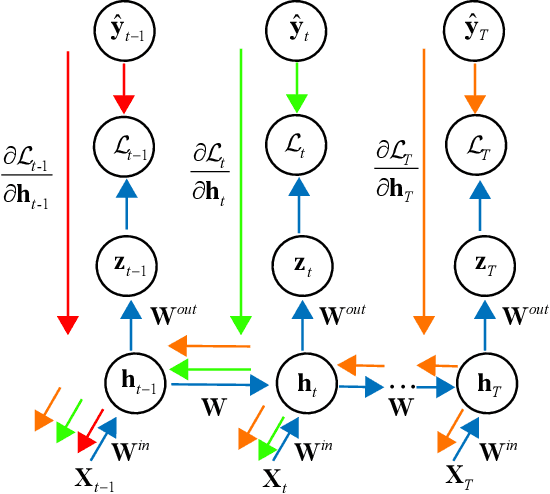
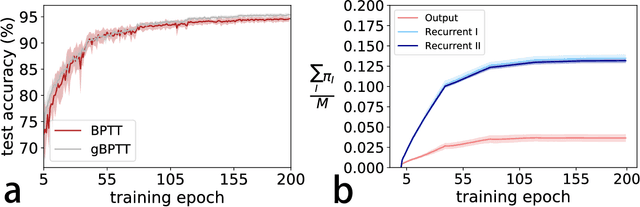
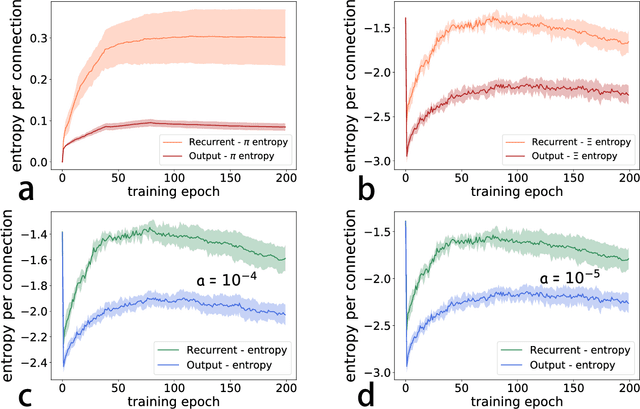
Ensemble perspective for understanding temporal credit assignment

Recurrent neural networks are widely used for modeling spatio-temporal sequences in both nature language processing and neural population dynamics. However, understanding the temporal credit assignment is hard. Here, we propose that each individual connection in the recurrent computation is modeled by a spike and slab distribution, rather than a precise weight value. We then derive the mean-field algorithm to train the network at the ensemble level. The method is then applied to classify handwritten digits when pixels are read in sequence, and to the multisensory integration task that is a fundamental cognitive function of animals. Our model reveals important connections that determine the overall performance of the network. The model also shows how spatio-temporal information is processed through the hyperparameters of the distribution, and moreover reveals distinct types of emergent neural selectivity. It is thus promising to study the temporal credit assignment in recurrent neural networks from the ensemble perspective.

Data-driven effective model shows a liquid-like deep learning

Geometric structure of an optimization landscape is argued to be fundamentally important to support the success of deep learning. However, recent research efforts focused on either of toy random models with unrealistic assumptions and numerical evidences about different shapes of the optimization landscape, thereby lacking a unified view about the nature of the landscape. Here, we propose a statistical mechanics framework by directly building a least structured model of the high-dimensional weight space, considering realistic structured data, stochastic gradient descent algorithms, and the computational depth of the network parametrized by weight parameters. We also consider whether the number of network parameters outnumbers the number of supplied training data, namely, over- or under-parametrization. Our least structured model predicts that the weight spaces of the under-parametrization and over-parameterization cases belong to the same class. These weight spaces are well-connected without any heterogeneous geometric properties. In contrast, the shallow-network has a shattered weight space, characterized by discontinuous phase transitions in physics, thereby clarifying roles of depth in deep learning. Our effective model also predicts that inside a deep network, there exists a liquid-like central part of the architecture in the sense that the weights in this part behave as randomly as possible. Our work may thus explain why deep learning is unreasonably effective in terms of the high-dimensional weight space, and how deep networks are different from shallow ones.