Advertising Media and Target Audience Optimization via High-dimensional Bandits

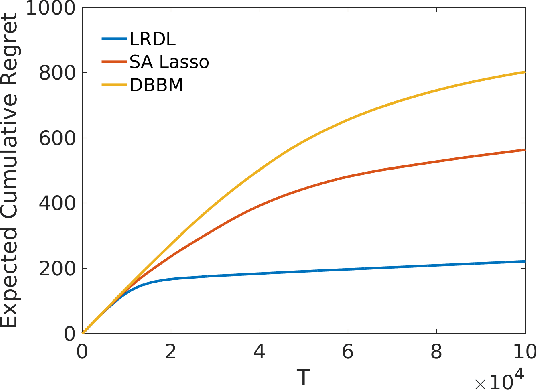
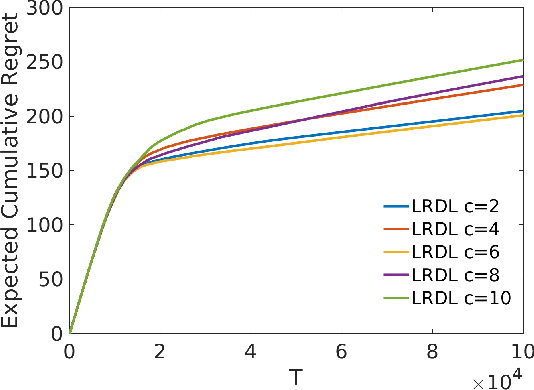
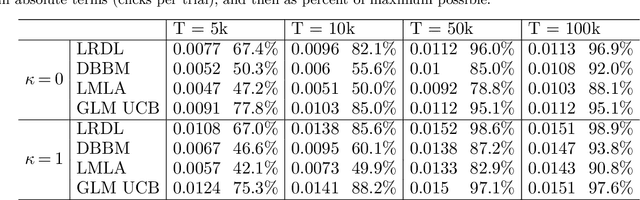
We present a data-driven algorithm that advertisers can use to automate their digital ad-campaigns at online publishers. The algorithm enables the advertiser to search across available target audiences and ad-media to find the best possible combination for its campaign via online experimentation. The problem of finding the best audience-ad combination is complicated by a number of distinctive challenges, including (a) a need for active exploration to resolve prior uncertainty and to speed the search for profitable combinations, (b) many combinations to choose from, giving rise to high-dimensional search formulations, and (c) very low success probabilities, typically just a fraction of one percent. Our algorithm (designated LRDL, an acronym for Logistic Regression with Debiased Lasso) addresses these challenges by combining four elements: a multiarmed bandit framework for active exploration; a Lasso penalty function to handle high dimensionality; an inbuilt debiasing kernel that handles the regularization bias induced by the Lasso; and a semi-parametric regression model for outcomes that promotes cross-learning across arms. The algorithm is implemented as a Thompson Sampler, and to the best of our knowledge, it is the first that can practically address all of the challenges above. Simulations with real and synthetic data show the method is effective and document its superior performance against several benchmarks from the recent high-dimensional bandit literature.

Optimal No-Regret Learning in Strongly Monotone Games with Bandit Feedback

We consider online no-regret learning in unknown games with bandit feedback, where each agent only observes its reward at each time -- determined by all players' current joint action -- rather than its gradient. We focus on the class of smooth and strongly monotone games and study optimal no-regret learning therein. Leveraging self-concordant barrier functions, we first construct an online bandit convex optimization algorithm and show that it achieves the single-agent optimal regret of $\tilde{\Theta}(\sqrt{T})$ under smooth and strongly-concave payoff functions. We then show that if each agent applies this no-regret learning algorithm in strongly monotone games, the joint action converges in \textit{last iterate} to the unique Nash equilibrium at a rate of $\tilde{\Theta}(1/\sqrt{T})$. Prior to our work, the best-know convergence rate in the same class of games is $O(1/T^{1/3})$ (achieved by a different algorithm), thus leaving open the problem of optimal no-regret learning algorithms (since the known lower bound is $\Omega(1/\sqrt{T})$). Our results thus settle this open problem and contribute to the broad landscape of bandit game-theoretical learning by identifying the first doubly optimal bandit learning algorithm, in that it achieves (up to log factors) both optimal regret in the single-agent learning and optimal last-iterate convergence rate in the multi-agent learning. We also present results on several simulation studies -- Cournot competition, Kelly auctions, and distributed regularized logistic regression -- to demonstrate the efficacy of our algorithm.