Stochastic Optimization for Vaccine and Testing Kit Allocation for the COVID-19 Pandemic

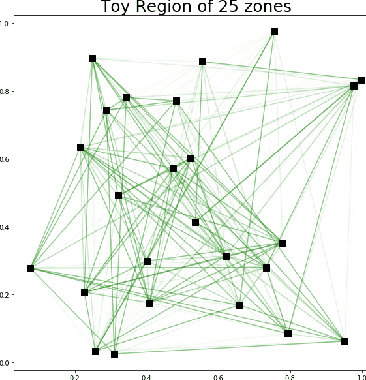
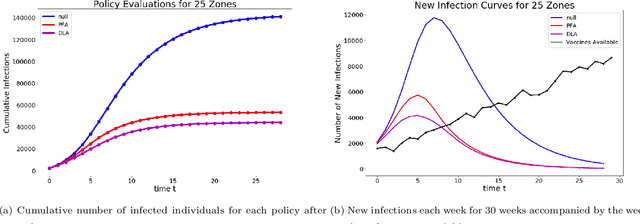
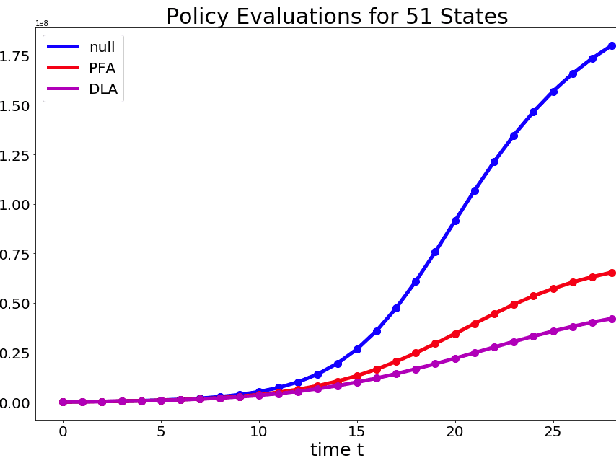
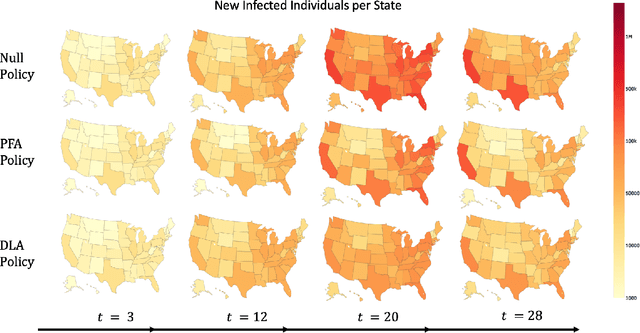
The pandemic caused by the SARS-CoV-2 virus has exposed many flaws in the decision-making strategies used to distribute resources to combat global health crises. In this paper, we leverage reinforcement learning and optimization to improve upon the allocation strategies for various resources. In particular, we consider a problem where a central controller must decide where to send testing kits to learn about the uncertain states of the world (active learning); then, use the new information to construct beliefs about the states and decide where to allocate resources. We propose a general model coupled with a tunable lookahead policy for making vaccine allocation decisions without perfect knowledge about the state of the world. The lookahead policy is compared to a population-based myopic policy which is more likely to be similar to the present strategies in practice. Each vaccine allocation policy works in conjunction with a testing kit allocation policy to perform active learning. Our simulation results demonstrate that an optimization-based lookahead decision making strategy will outperform the presented myopic policy.

Dynamic Bidding for Advance Commitments in Truckload Brokerage Markets

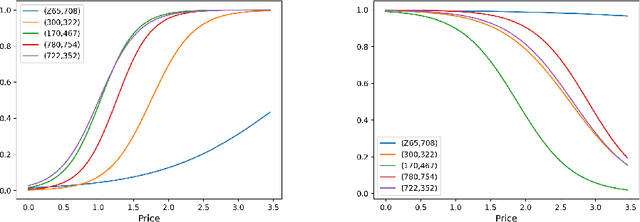
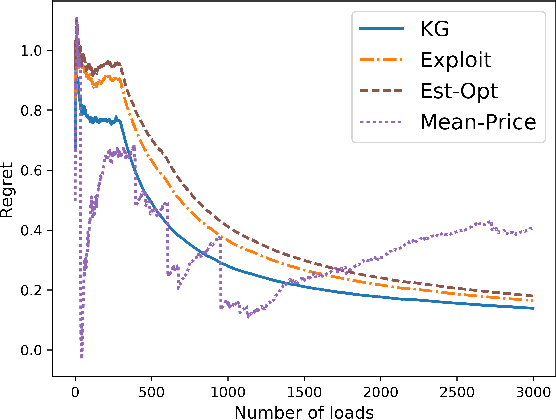
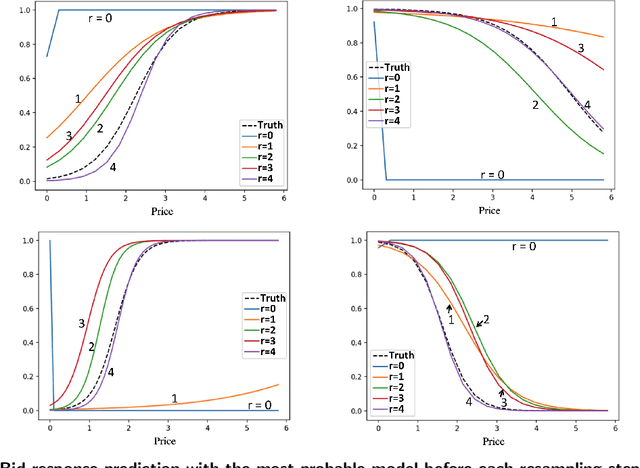
Truckload brokerages, a $100 billion/year industry in the U.S., plays the critical role of matching shippers with carriers, often to move loads several days into the future. Brokerages not only have to find companies that will agree to move a load, the brokerage often has to find a price that both the shipper and carrier will agree to. The price not only varies by shipper and carrier, but also by the traffic lanes and other variables such as commodity type. Brokerages have to learn about shipper and carrier response functions by offering a price and observing whether each accepts the quote. We propose a knowledge gradient policy with bootstrap aggregation for high-dimensional contextual settings to guide price experimentation by maximizing the value of information. The learning policy is tested using a newly developed, carefully calibrated fleet simulator that includes a stochastic lookahead policy that simulates fleet movements, as well as the stochastic modeling of driver assignments and the carrier's load commitment policies with advance booking.

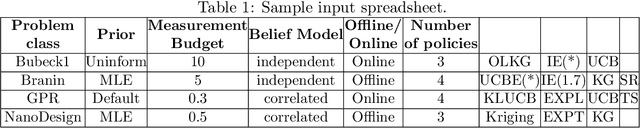
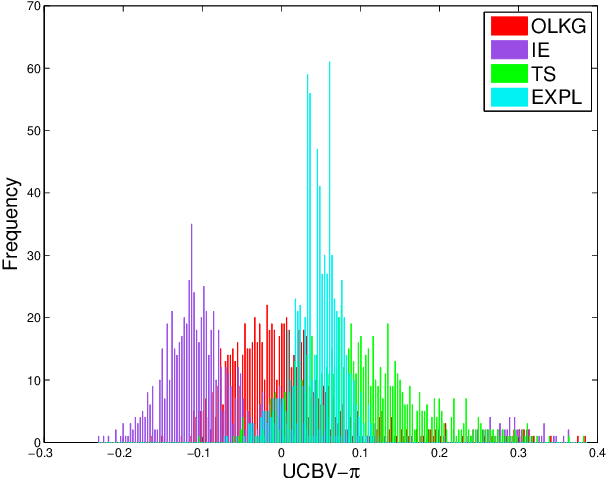
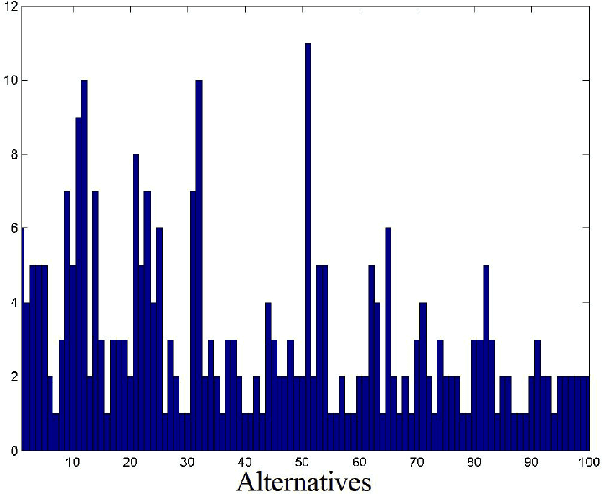
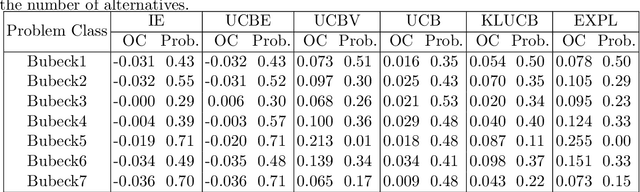
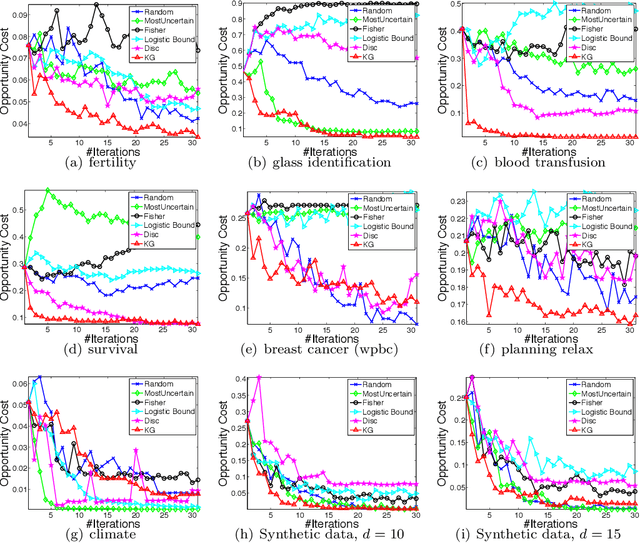
MOLTE: a Modular Optimal Learning Testing Environment

We address the relative paucity of empirical testing of learning algorithms (of any type) by introducing a new public-domain, Modular, Optimal Learning Testing Environment (MOLTE) for Bayesian ranking and selection problem, stochastic bandits or sequential experimental design problems. The Matlab-based simulator allows the comparison of a number of learning policies (represented as a series of .m modules) in the context of a wide range of problems (each represented in its own .m module) which makes it easy to add new algorithms and new test problems. State-of-the-art policies and various problem classes are provided in the package. The choice of problems and policies is guided through a spreadsheet-based interface. Different graphical metrics are included. MOLTE is designed to be compatible with parallel computing to scale up from local desktop to clusters and clouds. We offer MOLTE as an easy-to-use tool for the research community that will make it possible to perform much more comprehensive testing, spanning a broader selection of algorithms and test problems. We demonstrate the capabilities of MOLTE through a series of comparisons of policies on a starter library of test problems. We also address the problem of tuning and constructing priors that have been largely overlooked in optimal learning literature. We envision MOLTE as a modest spur to provide researchers an easy environment to study interesting questions involved in optimal learning.

Optimal Learning for Sequential Decision Making for Expensive Cost Functions with Stochastic Binary Feedbacks

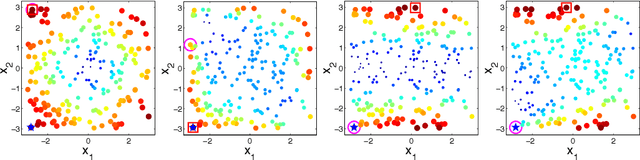
We consider the problem of sequentially making decisions that are rewarded by "successes" and "failures" which can be predicted through an unknown relationship that depends on a partially controllable vector of attributes for each instance. The learner takes an active role in selecting samples from the instance pool. The goal is to maximize the probability of success in either offline (training) or online (testing) phases. Our problem is motivated by real-world applications where observations are time-consuming and/or expensive. We develop a knowledge gradient policy using an online Bayesian linear classifier to guide the experiment by maximizing the expected value of information of labeling each alternative. We provide a finite-time analysis of the estimated error and show that the maximum likelihood estimator based produced by the KG policy is consistent and asymptotically normal. We also show that the knowledge gradient policy is asymptotically optimal in an offline setting. This work further extends the knowledge gradient to the setting of contextual bandits. We report the results of a series of experiments that demonstrate its efficiency.

An optimal learning method for developing personalized treatment regimes

A treatment regime is a function that maps individual patient information to a recommended treatment, hence explicitly incorporating the heterogeneity in need for treatment across individuals. Patient responses are dichotomous and can be predicted through an unknown relationship that depends on the patient information and the selected treatment. The goal is to find the treatments that lead to the best patient responses on average. Each experiment is expensive, forcing us to learn the most from each experiment. We adopt a Bayesian approach both to incorporate possible prior information and to update our treatment regime continuously as information accrues, with the potential to allow smaller yet more informative trials and for patients to receive better treatment. By formulating the problem as contextual bandits, we introduce a knowledge gradient policy to guide the treatment assignment by maximizing the expected value of information, for which an approximation method is used to overcome computational challenges. We provide a detailed study on how to make sequential medical decisions under uncertainty to reduce health care costs on a real world knee replacement dataset. We use clustering and LASSO to deal with the intrinsic sparsity in health datasets. We show experimentally that even though the problem is sparse, through careful selection of physicians (versus picking them at random), we can significantly improve the success rates.

Finite-time Analysis for the Knowledge-Gradient Policy

We consider sequential decision problems in which we adaptively choose one of finitely many alternatives and observe a stochastic reward. We offer a new perspective of interpreting Bayesian ranking and selection problems as adaptive stochastic multi-set maximization problems and derive the first finite-time bound of the knowledge-gradient policy for adaptive submodular objective functions. In addition, we introduce the concept of prior-optimality and provide another insight into the performance of the knowledge gradient policy based on the submodular assumption on the value of information. We demonstrate submodularity for the two-alternative case and provide other conditions for more general problems, bringing out the issue and importance of submodularity in learning problems. Empirical experiments are conducted to further illustrate the finite time behavior of the knowledge gradient policy.

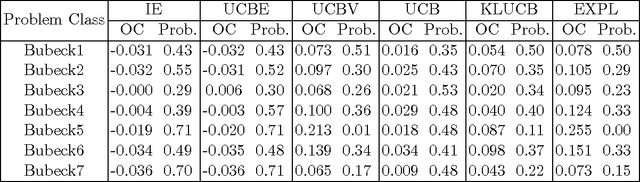
The Knowledge Gradient with Logistic Belief Models for Binary Classification

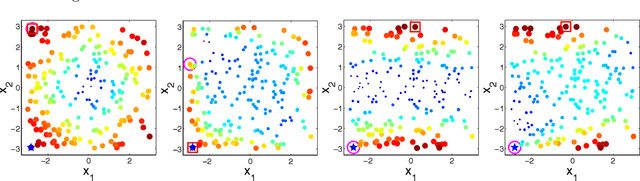
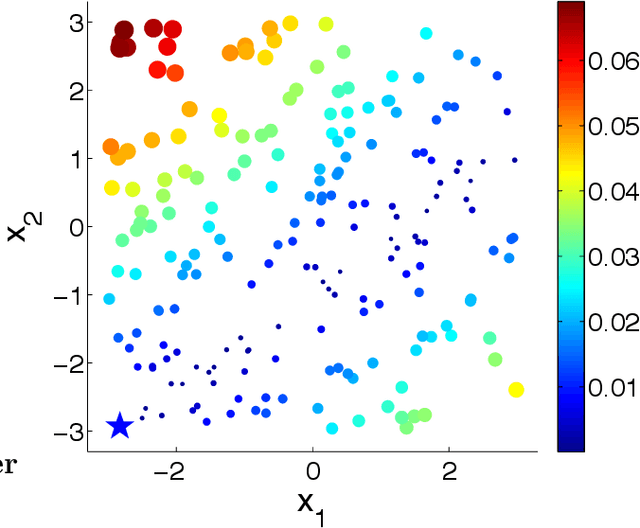
We consider sequential decision making problems for binary classification scenario in which the learner takes an active role in repeatedly selecting samples from the action pool and receives the binary label of the selected alternatives. Our problem is motivated by applications where observations are time consuming and/or expensive, resulting in small samples. The goal is to identify the best alternative with the highest response. We use Bayesian logistic regression to predict the response of each alternative. By formulating the problem as a Markov decision process, we develop a knowledge-gradient type policy to guide the experiment by maximizing the expected value of information of labeling each alternative and provide a finite-time analysis on the estimated error. Experiments on benchmark UCI datasets demonstrate the effectiveness of the proposed method.

The Knowledge Gradient Policy Using A Sparse Additive Belief Model

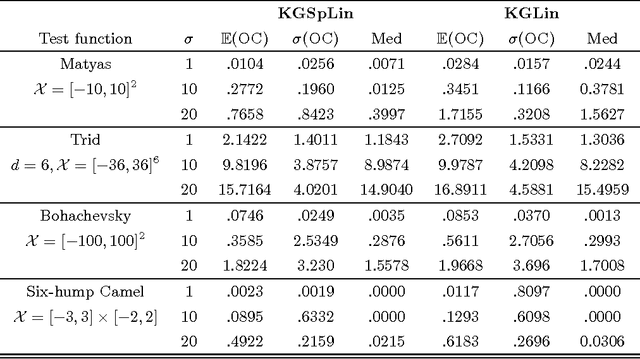
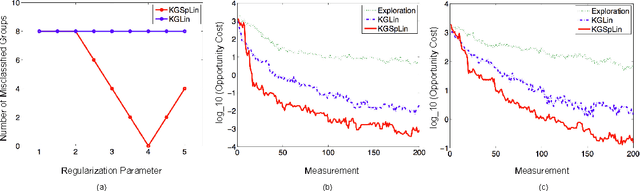
We propose a sequential learning policy for noisy discrete global optimization and ranking and selection (R\&S) problems with high dimensional sparse belief functions, where there are hundreds or even thousands of features, but only a small portion of these features contain explanatory power. We aim to identify the sparsity pattern and select the best alternative before the finite budget is exhausted. We derive a knowledge gradient policy for sparse linear models (KGSpLin) with group Lasso penalty. This policy is a unique and novel hybrid of Bayesian R\&S with frequentist learning. Particularly, our method naturally combines B-spline basis expansion and generalizes to the nonparametric additive model (KGSpAM) and functional ANOVA model. Theoretically, we provide the estimation error bounds of the posterior mean estimate and the functional estimate. Controlled experiments show that the algorithm efficiently learns the correct set of nonzero parameters even when the model is imbedded with hundreds of dummy parameters. Also it outperforms the knowledge gradient for a linear model.