An optimal learning method for developing personalized treatment regimes
Paper and Code
Jul 06, 2016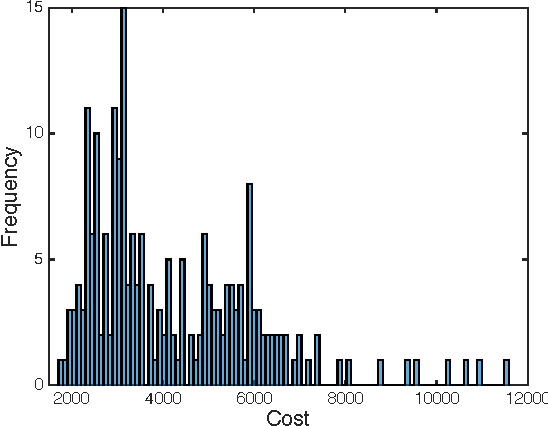
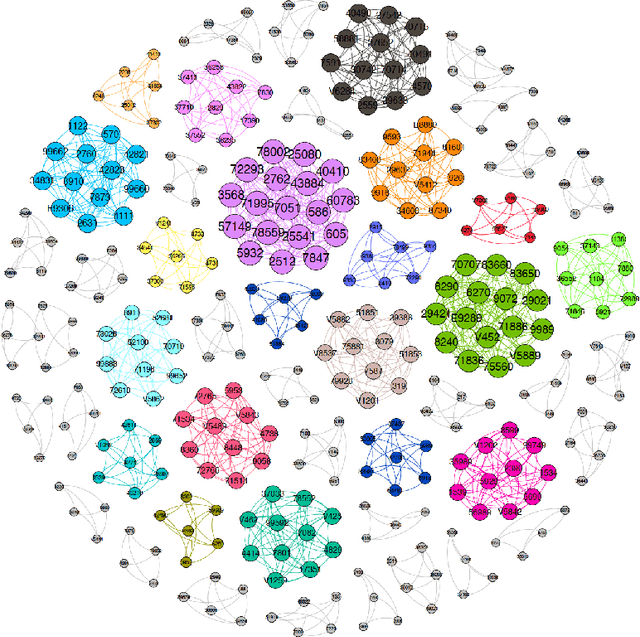
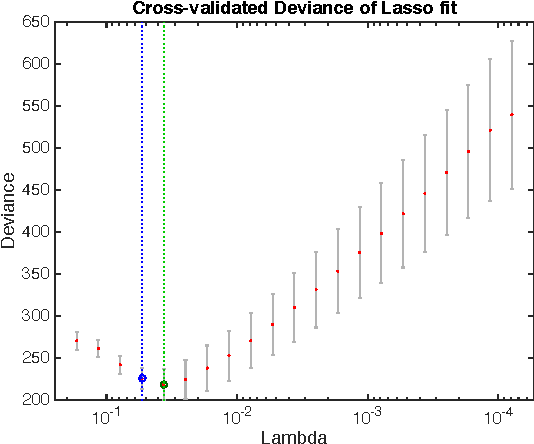

A treatment regime is a function that maps individual patient information to a recommended treatment, hence explicitly incorporating the heterogeneity in need for treatment across individuals. Patient responses are dichotomous and can be predicted through an unknown relationship that depends on the patient information and the selected treatment. The goal is to find the treatments that lead to the best patient responses on average. Each experiment is expensive, forcing us to learn the most from each experiment. We adopt a Bayesian approach both to incorporate possible prior information and to update our treatment regime continuously as information accrues, with the potential to allow smaller yet more informative trials and for patients to receive better treatment. By formulating the problem as contextual bandits, we introduce a knowledge gradient policy to guide the treatment assignment by maximizing the expected value of information, for which an approximation method is used to overcome computational challenges. We provide a detailed study on how to make sequential medical decisions under uncertainty to reduce health care costs on a real world knee replacement dataset. We use clustering and LASSO to deal with the intrinsic sparsity in health datasets. We show experimentally that even though the problem is sparse, through careful selection of physicians (versus picking them at random), we can significantly improve the success rates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge