Finite-time Analysis for the Knowledge-Gradient Policy
Paper and Code
Jun 15, 2016
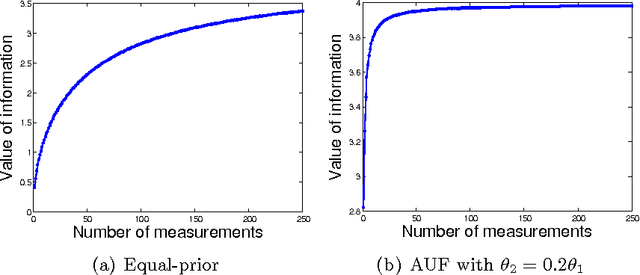
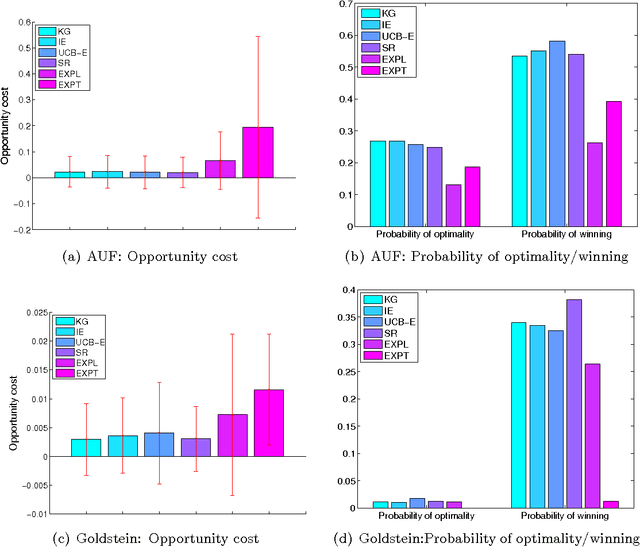
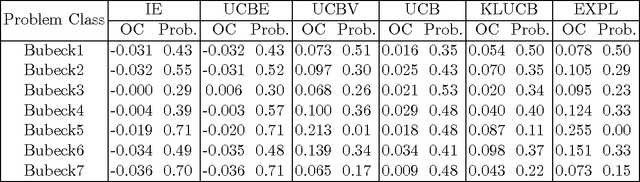
We consider sequential decision problems in which we adaptively choose one of finitely many alternatives and observe a stochastic reward. We offer a new perspective of interpreting Bayesian ranking and selection problems as adaptive stochastic multi-set maximization problems and derive the first finite-time bound of the knowledge-gradient policy for adaptive submodular objective functions. In addition, we introduce the concept of prior-optimality and provide another insight into the performance of the knowledge gradient policy based on the submodular assumption on the value of information. We demonstrate submodularity for the two-alternative case and provide other conditions for more general problems, bringing out the issue and importance of submodularity in learning problems. Empirical experiments are conducted to further illustrate the finite time behavior of the knowledge gradient policy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge