The Knowledge Gradient Policy Using A Sparse Additive Belief Model
Paper and Code
Mar 18, 2015
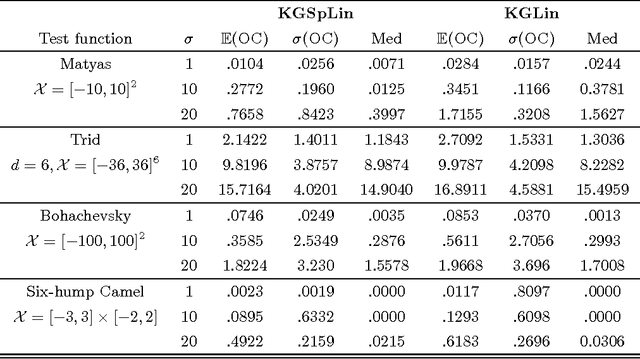
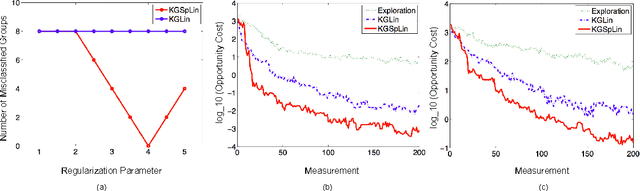

We propose a sequential learning policy for noisy discrete global optimization and ranking and selection (R\&S) problems with high dimensional sparse belief functions, where there are hundreds or even thousands of features, but only a small portion of these features contain explanatory power. We aim to identify the sparsity pattern and select the best alternative before the finite budget is exhausted. We derive a knowledge gradient policy for sparse linear models (KGSpLin) with group Lasso penalty. This policy is a unique and novel hybrid of Bayesian R\&S with frequentist learning. Particularly, our method naturally combines B-spline basis expansion and generalizes to the nonparametric additive model (KGSpAM) and functional ANOVA model. Theoretically, we provide the estimation error bounds of the posterior mean estimate and the functional estimate. Controlled experiments show that the algorithm efficiently learns the correct set of nonzero parameters even when the model is imbedded with hundreds of dummy parameters. Also it outperforms the knowledge gradient for a linear model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge