A Perspective on Large Language Models, Intelligent Machines, and Knowledge Acquisition

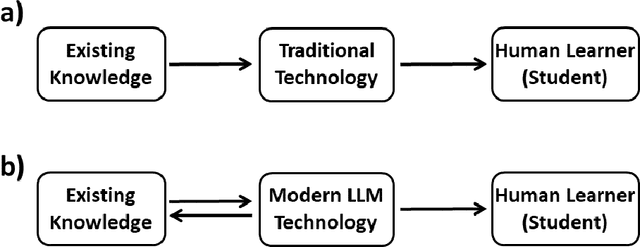
Large Language Models (LLMs) are known for their remarkable ability to generate synthesized 'knowledge', such as text documents, music, images, etc. However, there is a huge gap between LLM's and human capabilities for understanding abstract concepts and reasoning. We discuss these issues in a larger philosophical context of human knowledge acquisition and the Turing test. In addition, we illustrate the limitations of LLMs by analyzing GPT-4 responses to questions ranging from science and math to common sense reasoning. These examples show that GPT-4 can often imitate human reasoning, even though it lacks understanding. However, LLM responses are synthesized from a large LLM model trained on all available data. In contrast, human understanding is based on a small number of abstract concepts. Based on this distinction, we discuss the impact of LLMs on acquisition of human knowledge and education.

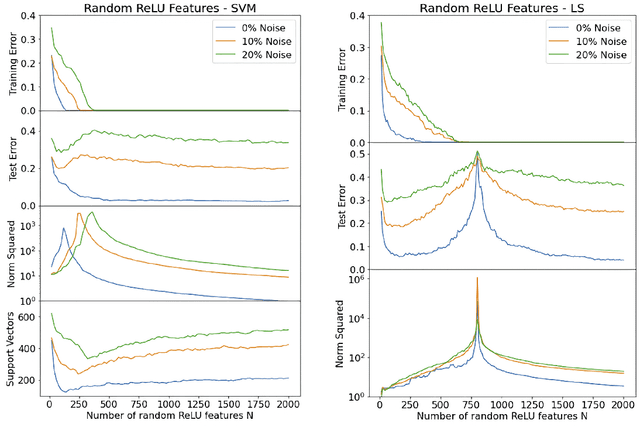
VC Theoretical Explanation of Double Descent

There has been growing interest in generalization performance of large multilayer neural networks that can be trained to achieve zero training error, while generalizing well on test data. This regime is known as 'second descent' and it appears to contradict conventional view that optimal model complexity should reflect optimal balance between underfitting and overfitting, aka the bias-variance trade-off. This paper presents VC-theoretical analysis of double descent and shows that it can be fully explained by classical VC generalization bounds. We illustrate an application of analytic VC-bounds for modeling double descent for classification problems, using empirical results for several learning methods, such as SVM, Least Squares, and Multilayer Perceptron classifiers. In addition, we discuss several possible reasons for misinterpretation of VC-theoretical results in the machine learning community.

Single Class Universum-SVM

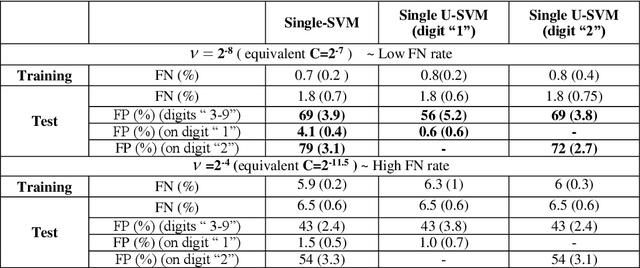
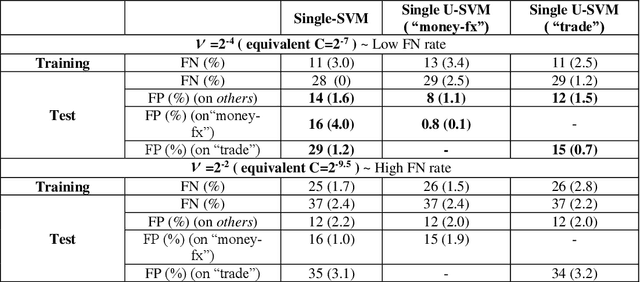
This paper extends the idea of Universum learning [1, 2] to single-class learning problems. We propose Single Class Universum-SVM setting that incorporates a priori knowledge (in the form of additional data samples) into the single class estimation problem. These additional data samples or Universum belong to the same application domain as (positive) data samples from a single class (of interest), but they follow a different distribution. Proposed methodology for single class U-SVM is based on the known connection between binary classification and single class learning formulations [3]. Several empirical comparisons are presented to illustrate the utility of the proposed approach.

Multiclass Universum SVM

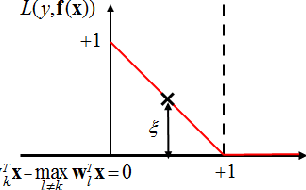
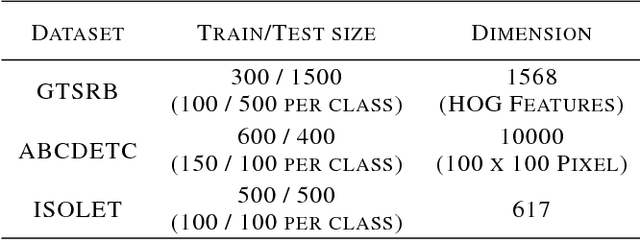
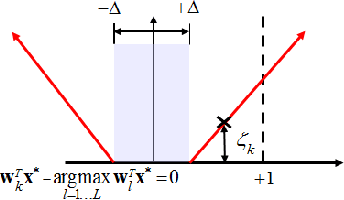
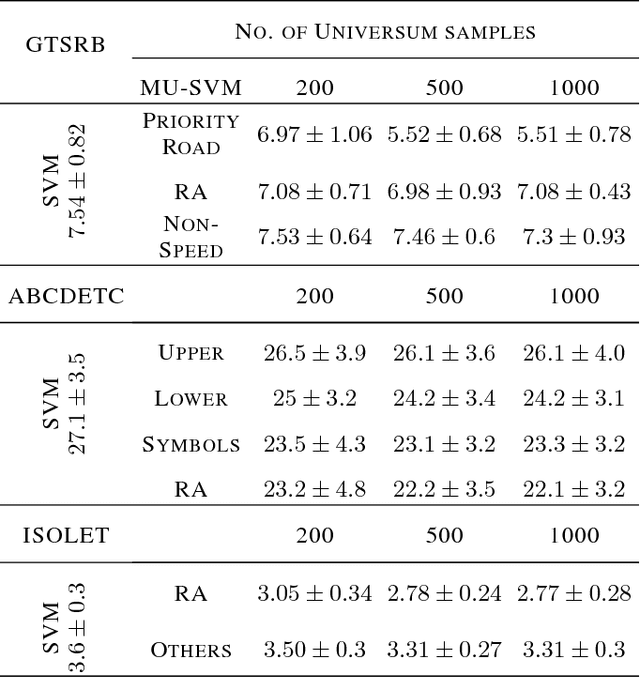
We introduce Universum learning for multiclass problems and propose a novel formulation for multiclass universum SVM (MU-SVM). We also propose an analytic span bound for model selection with almost 2-4x faster computation times than standard resampling techniques. We empirically demonstrate the efficacy of the proposed MUSVM formulation on several real world datasets achieving > 20% improvement in test accuracies compared to multi-class SVM.

Universum Learning for Multiclass SVM

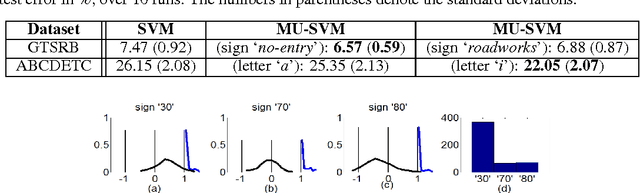
We introduce Universum learning for multiclass problems and propose a novel formulation for multiclass universum SVM (MU-SVM). We also propose a span bound for MU-SVM that can be used for model selection thereby avoiding resampling. Empirical results demonstrate the effectiveness of MU-SVM and the proposed bound.

Universum Learning for SVM Regression

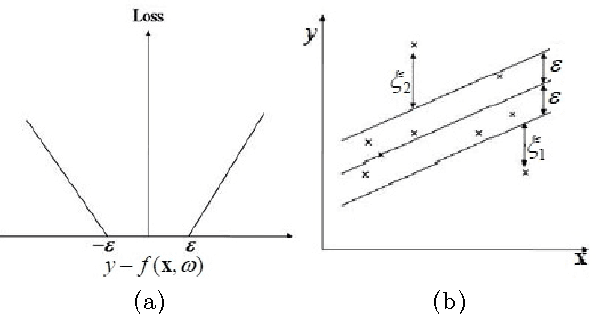
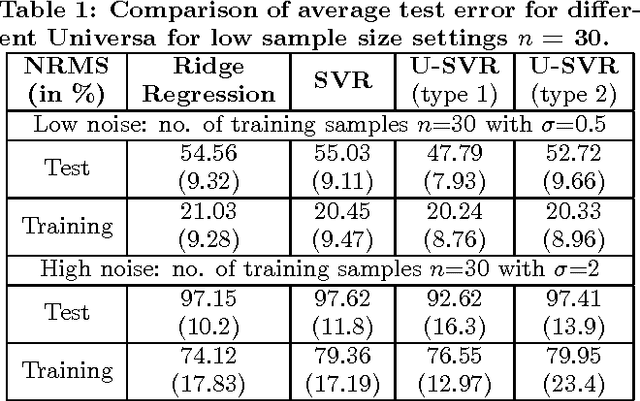
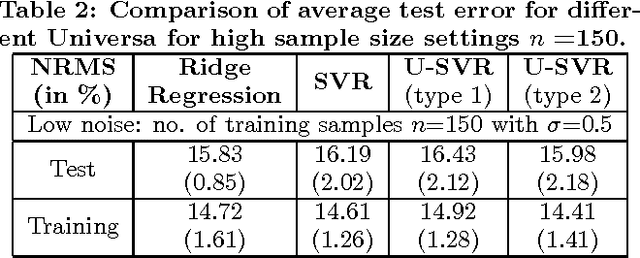
This paper extends the idea of Universum learning [18, 19] to regression problems. We propose new Universum-SVM formulation for regression problems that incorporates a priori knowledge in the form of additional data samples. These additional data samples or Universum belong to the same application domain as the training samples, but they follow a different distribution. Several empirical comparisons are presented to illustrate the utility of the proposed approach.