VC Theoretical Explanation of Double Descent
Paper and Code
May 31, 2022


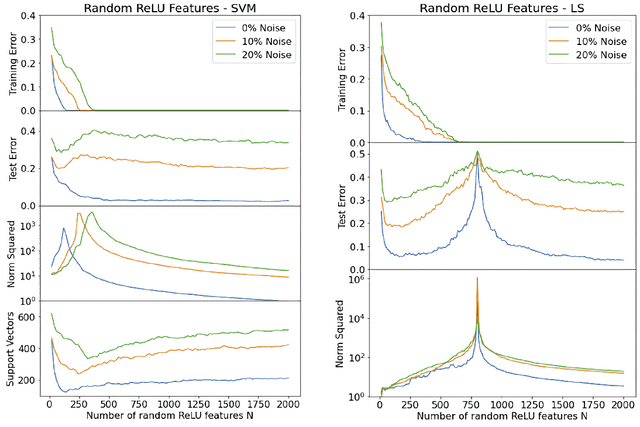
There has been growing interest in generalization performance of large multilayer neural networks that can be trained to achieve zero training error, while generalizing well on test data. This regime is known as 'second descent' and it appears to contradict conventional view that optimal model complexity should reflect optimal balance between underfitting and overfitting, aka the bias-variance trade-off. This paper presents VC-theoretical analysis of double descent and shows that it can be fully explained by classical VC generalization bounds. We illustrate an application of analytic VC-bounds for modeling double descent for classification problems, using empirical results for several learning methods, such as SVM, Least Squares, and Multilayer Perceptron classifiers. In addition, we discuss several possible reasons for misinterpretation of VC-theoretical results in the machine learning community.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge