Vishal Bindal
Learning to Recover from Plan Execution Errors during Robot Manipulation: A Neuro-symbolic Approach
May 29, 2024

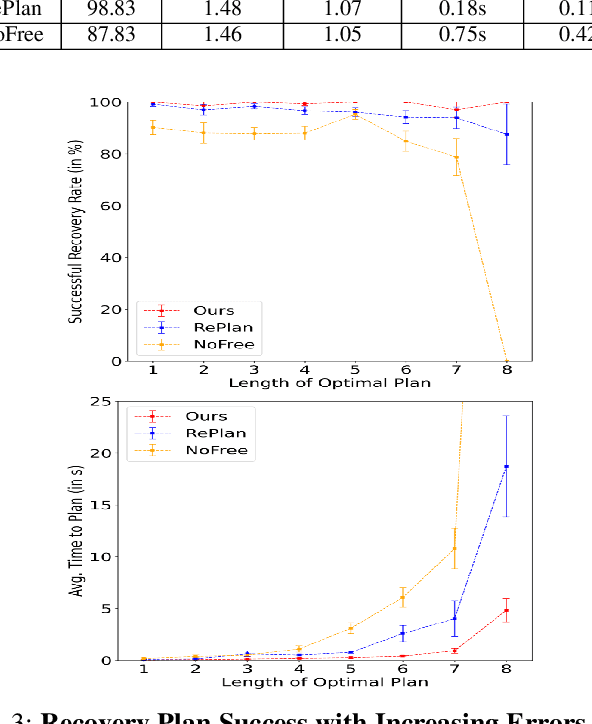

Abstract:Automatically detecting and recovering from failures is an important but challenging problem for autonomous robots. Most of the recent work on learning to plan from demonstrations lacks the ability to detect and recover from errors in the absence of an explicit state representation and/or a (sub-) goal check function. We propose an approach (blending learning with symbolic search) for automated error discovery and recovery, without needing annotated data of failures. Central to our approach is a neuro-symbolic state representation, in the form of dense scene graph, structured based on the objects present within the environment. This enables efficient learning of the transition function and a discriminator that not only identifies failures but also localizes them facilitating fast re-planning via computation of heuristic distance function. We also present an anytime version of our algorithm, where instead of recovering to the last correct state, we search for a sub-goal in the original plan minimizing the total distance to the goal given a re-planning budget. Experiments on a physics simulator with a variety of simulated failures show the effectiveness of our approach compared to existing baselines, both in terms of efficiency as well as accuracy of our recovery mechanism.
Sketch-Plan-Generalize: Continual Few-Shot Learning of Inductively Generalizable Spatial Concepts for Language-Guided Robot Manipulation
Apr 11, 2024



Abstract:Our goal is to build embodied agents that can learn inductively generalizable spatial concepts in a continual manner, e.g, constructing a tower of a given height. Existing work suffers from certain limitations (a) (Liang et al., 2023) and their multi-modal extensions, rely heavily on prior knowledge and are not grounded in the demonstrations (b) (Liu et al., 2023) lack the ability to generalize due to their purely neural approach. A key challenge is to achieve a fine balance between symbolic representations which have the capability to generalize, and neural representations that are physically grounded. In response, we propose a neuro-symbolic approach by expressing inductive concepts as symbolic compositions over grounded neural concepts. Our key insight is to decompose the concept learning problem into the following steps 1) Sketch: Getting a programmatic representation for the given instruction 2) Plan: Perform Model-Based RL over the sequence of grounded neural action concepts to learn a grounded plan 3) Generalize: Abstract out a generic (lifted) Python program to facilitate generalizability. Continual learning is achieved by interspersing learning of grounded neural concepts with higher level symbolic constructs. Our experiments demonstrate that our approach significantly outperforms existing baselines in terms of its ability to learn novel concepts and generalize inductively.
Learning Neuro-symbolic Programs for Language Guided Robot Manipulation
Nov 12, 2022



Abstract:Given a natural language instruction, and an input and an output scene, our goal is to train a neuro-symbolic model which can output a manipulation program that can be executed by the robot on the input scene resulting in the desired output scene. Prior approaches for this task possess one of the following limitations: (i) rely on hand-coded symbols for concepts limiting generalization beyond those seen during training [1] (ii) infer action sequences from instructions but require dense sub-goal supervision [2] or (iii) lack semantics required for deeper object-centric reasoning inherent in interpreting complex instructions [3]. In contrast, our approach is neuro-symbolic and can handle linguistic as well as perceptual variations, is end-to-end differentiable requiring no intermediate supervision, and makes use of symbolic reasoning constructs which operate on a latent neural object-centric representation, allowing for deeper reasoning over the input scene. Central to our approach is a modular structure, consisting of a hierarchical instruction parser, and a manipulation module to learn disentangled action representations, both trained via RL. Our experiments on a simulated environment with a 7-DOF manipulator, consisting of instructions with varying number of steps, as well as scenes with different number of objects, and objects with unseen attribute combinations, demonstrate that our model is robust to such variations, and significantly outperforms existing baselines, particularly in generalization settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge