Enhancing Edge Intelligence with Highly Discriminant LNT Features

AI algorithms at the edge demand smaller model sizes and lower computational complexity. To achieve these objectives, we adopt a green learning (GL) paradigm rather than the deep learning paradigm. GL has three modules: 1) unsupervised representation learning, 2) supervised feature learning, and 3) supervised decision learning. We focus on the second module in this work. In particular, we derive new discriminant features from proper linear combinations of input features, denoted by x, obtained in the first module. They are called complementary and raw features, respectively. Along this line, we present a novel supervised learning method to generate highly discriminant complementary features based on the least-squares normal transform (LNT). LNT consists of two steps. First, we convert a C-class classification problem to a binary classification problem. The two classes are assigned with 0 and 1, respectively. Next, we formulate a least-squares regression problem from the N-dimensional (N-D) feature space to the 1-D output space, and solve the least-squares normal equation to obtain one N-D normal vector, denoted by a1. Since one normal vector is yielded by one binary split, we can obtain M normal vectors with M splits. Then, Ax is called an LNT of x, where transform matrix A in R^{M by N} by stacking aj^T, j=1, ..., M, and the LNT, Ax, can generate M new features. The newly generated complementary features are shown to be more discriminant than the raw features. Experiments show that the classification performance can be improved by these new features.

Acceleration of Subspace Learning Machine via Particle Swarm Optimization and Parallel Processing

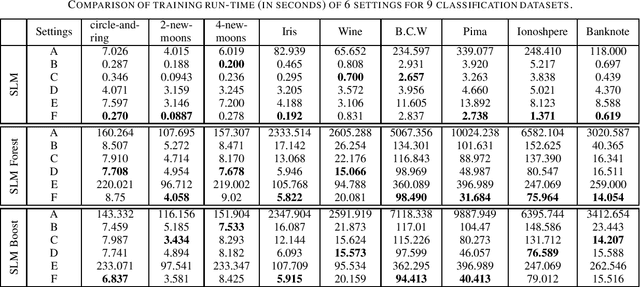
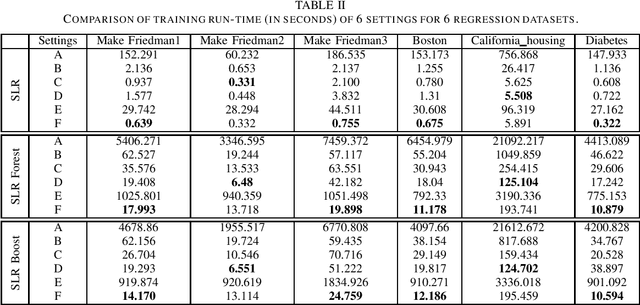
Built upon the decision tree (DT) classification and regression idea, the subspace learning machine (SLM) has been recently proposed to offer higher performance in general classification and regression tasks. Its performance improvement is reached at the expense of higher computational complexity. In this work, we investigate two ways to accelerate SLM. First, we adopt the particle swarm optimization (PSO) algorithm to speed up the search of a discriminant dimension that is expressed as a linear combination of current dimensions. The search of optimal weights in the linear combination is computationally heavy. It is accomplished by probabilistic search in original SLM. The acceleration of SLM by PSO requires 10-20 times fewer iterations. Second, we leverage parallel processing in the SLM implementation. Experimental results show that the accelerated SLM method achieves a speed up factor of 577 in training time while maintaining comparable classification/regression performance of original SLM.

Subspace Learning Machine (SLM): Methodology and Performance

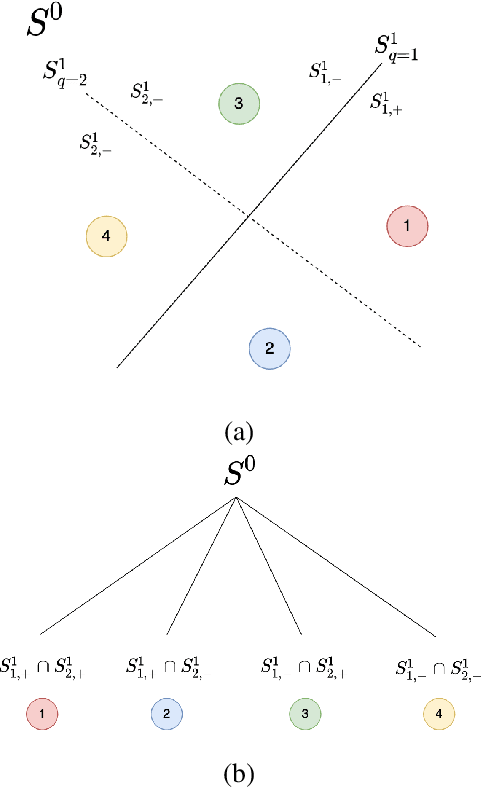
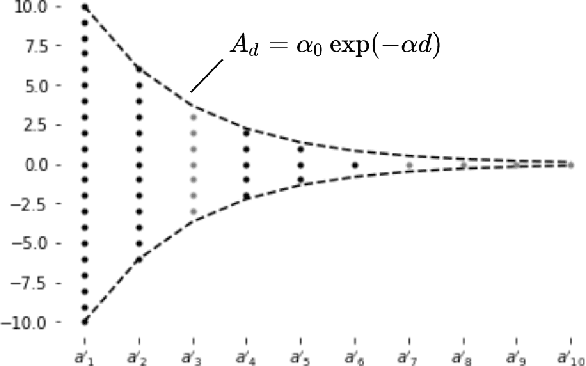
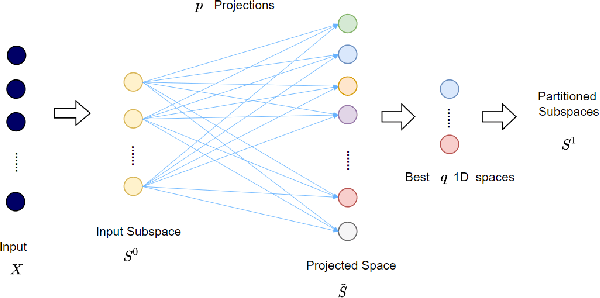
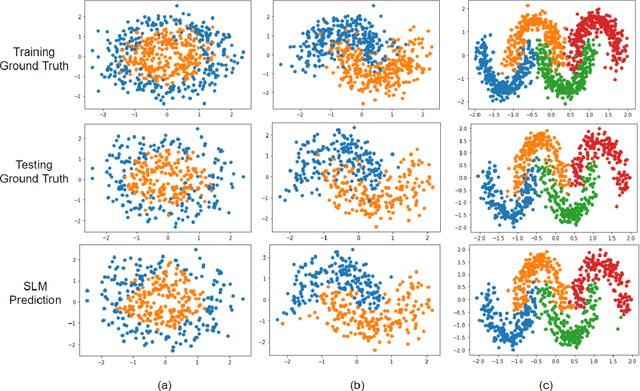
Inspired by the feedforward multilayer perceptron (FF-MLP), decision tree (DT) and extreme learning machine (ELM), a new classification model, called the subspace learning machine (SLM), is proposed in this work. SLM first identifies a discriminant subspace, $S^0$, by examining the discriminant power of each input feature. Then, it uses probabilistic projections of features in $S^0$ to yield 1D subspaces and finds the optimal partition for each of them. This is equivalent to partitioning $S^0$ with hyperplanes. A criterion is developed to choose the best $q$ partitions that yield $2q$ partitioned subspaces among them. We assign $S^0$ to the root node of a decision tree and the intersections of $2q$ subspaces to its child nodes of depth one. The partitioning process is recursively applied at each child node to build an SLM tree. When the samples at a child node are sufficiently pure, the partitioning process stops and each leaf node makes a prediction. The idea can be generalized to regression, leading to the subspace learning regressor (SLR). Furthermore, ensembles of SLM/SLR trees can yield a stronger predictor. Extensive experiments are conducted for performance benchmarking among SLM/SLR trees, ensembles and classical classifiers/regressors.