Subspace Learning Machine (SLM): Methodology and Performance
Paper and Code
May 11, 2022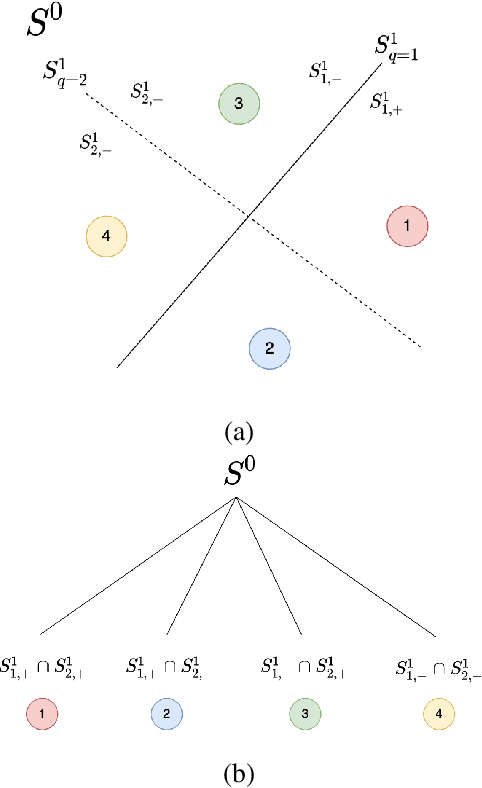
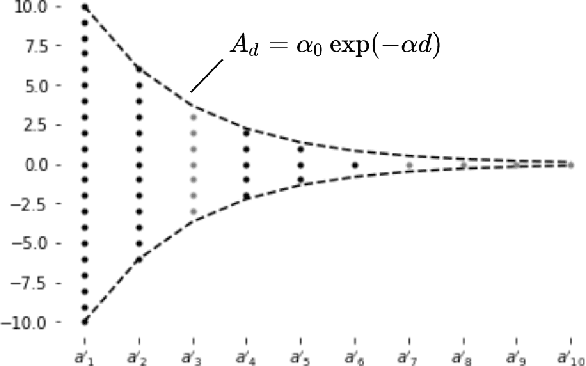
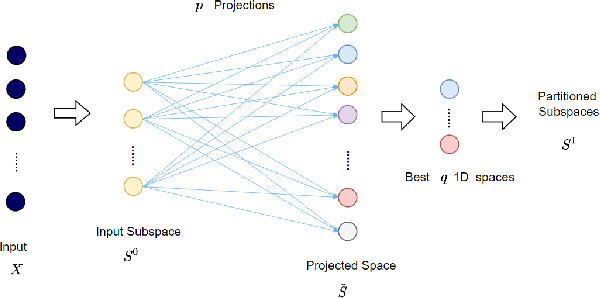
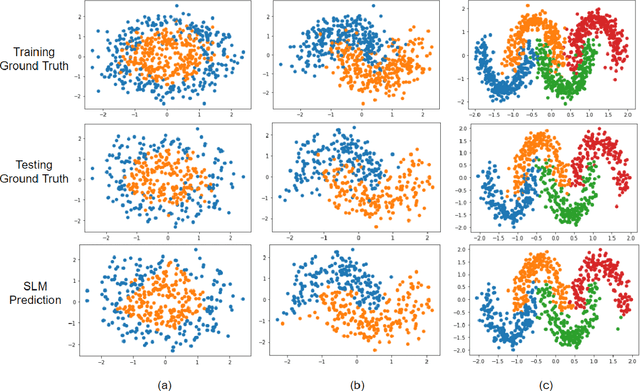
Inspired by the feedforward multilayer perceptron (FF-MLP), decision tree (DT) and extreme learning machine (ELM), a new classification model, called the subspace learning machine (SLM), is proposed in this work. SLM first identifies a discriminant subspace, $S^0$, by examining the discriminant power of each input feature. Then, it uses probabilistic projections of features in $S^0$ to yield 1D subspaces and finds the optimal partition for each of them. This is equivalent to partitioning $S^0$ with hyperplanes. A criterion is developed to choose the best $q$ partitions that yield $2q$ partitioned subspaces among them. We assign $S^0$ to the root node of a decision tree and the intersections of $2q$ subspaces to its child nodes of depth one. The partitioning process is recursively applied at each child node to build an SLM tree. When the samples at a child node are sufficiently pure, the partitioning process stops and each leaf node makes a prediction. The idea can be generalized to regression, leading to the subspace learning regressor (SLR). Furthermore, ensembles of SLM/SLR trees can yield a stronger predictor. Extensive experiments are conducted for performance benchmarking among SLM/SLR trees, ensembles and classical classifiers/regressors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge