Inference of Sequential Patterns for Neural Message Passing in Temporal Graphs

The modelling of temporal patterns in dynamic graphs is an important current research issue in the development of time-aware GNNs. Whether or not a specific sequence of events in a temporal graph constitutes a temporal pattern not only depends on the frequency of its occurrence. We consider whether it deviates from what is expected in a temporal graph where timestamps are randomly shuffled. While accounting for such a random baseline is important to model temporal patterns, it has mostly been ignored by current temporal graph neural networks. To address this issue we propose HYPA-DBGNN, a novel two-step approach that combines (i) the inference of anomalous sequential patterns in time series data on graphs based on a statistically principled null model, with (ii) a neural message passing approach that utilizes a higher-order De Bruijn graph whose edges capture overrepresented sequential patterns. Our method leverages hypergeometric graph ensembles to identify anomalous edges within both first- and higher-order De Bruijn graphs, which encode the temporal ordering of events. The model introduces an inductive bias that enhances model interpretability. We evaluate our approach for static node classification using benchmark datasets and a synthetic dataset that showcases its ability to incorporate the observed inductive bias regarding over- and under-represented temporal edges. We demonstrate the framework's effectiveness in detecting similar patterns within empirical datasets, resulting in superior performance compared to baseline methods in node classification tasks. To the best of our knowledge, our work is the first to introduce statistically informed GNNs that leverage temporal and causal sequence anomalies. HYPA-DBGNN represents a path for bridging the gap between statistical graph inference and neural graph representation learning, with potential applications to static GNNs.

Bayesian Detection of Mesoscale Structures in Pathway Data on Graphs

Mesoscale structures are an integral part of the abstraction and analysis of complex systems. They reveal a node's function in the network, and facilitate our understanding of the network dynamics. For example, they can represent communities in social or citation networks, roles in corporate interactions, or core-periphery structures in transportation networks. We usually detect mesoscale structures under the assumption of independence of interactions. Still, in many cases, the interactions invalidate this assumption by occurring in a specific order. Such patterns emerge in pathway data; to capture them, we have to model the dependencies between interactions using higher-order network models. However, the detection of mesoscale structures in higher-order networks is still under-researched. In this work, we derive a Bayesian approach that simultaneously models the optimal partitioning of nodes in groups and the optimal higher-order network dynamics between the groups. In synthetic data we demonstrate that our method can recover both standard proximity-based communities and role-based groupings of nodes. In synthetic and real world data we show that it can compete with baseline techniques, while additionally providing interpretable abstractions of network dynamics.

Bayesian Inference of Transition Matrices from Incomplete Graph Data with a Topological Prior

Many network analysis and graph learning techniques are based on models of random walks which require to infer transition matrices that formalize the underlying stochastic process in an observed graph. For weighted graphs, it is common to estimate the entries of such transition matrices based on the relative weights of edges. However, we are often confronted with incomplete data, which turns the construction of the transition matrix based on a weighted graph into an inference problem. Moreover, we often have access to additional information, which capture topological constraints of the system, i.e. which edges in a weighted graph are (theoretically) possible and which are not, e.g. transportation networks, where we have access to passenger trajectories as well as the physical topology of connections, or a set of social interactions with the underlying social structure. Combining these two different sources of information to infer transition matrices is an open challenge, with implications on the downstream network analysis tasks. Addressing this issue, we show that including knowledge on such topological constraints can improve the inference of transition matrices, especially for small datasets. We derive an analytically tractable Bayesian method that uses repeated interactions and a topological prior to infer transition matrices data-efficiently. We compare it against commonly used frequentist and Bayesian approaches both in synthetic and real-world datasets, and we find that it recovers the transition probabilities with higher accuracy and that it is robust even in cases when the knowledge of the topological constraint is partial. Lastly, we show that this higher accuracy improves the results for downstream network analysis tasks like cluster detection and node ranking, which highlights the practical relevance of our method for analyses of various networked systems.

One Graph to Rule them All: Using NLP and Graph Neural Networks to analyse Tolkien's Legendarium

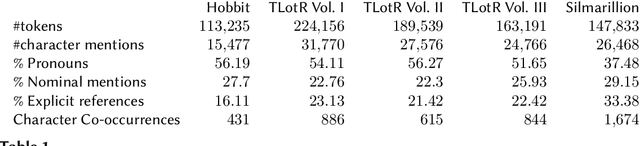
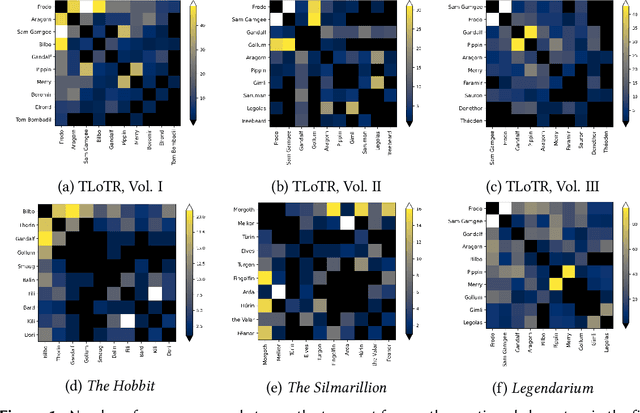
Natural Language Processing and Machine Learning have considerably advanced Computational Literary Studies. Similarly, the construction of co-occurrence networks of literary characters, and their analysis using methods from social network analysis and network science, have provided insights into the micro- and macro-level structure of literary texts. Combining these perspectives, in this work we study character networks extracted from a text corpus of J.R.R. Tolkien's Legendarium. We show that this perspective helps us to analyse and visualise the narrative style that characterises Tolkien's works. Addressing character classification, embedding and co-occurrence prediction, we further investigate the advantages of state-of-the-art Graph Neural Networks over a popular word embedding method. Our results highlight the large potential of graph learning in Computational Literary Studies.

De Bruijn goes Neural: Causality-Aware Graph Neural Networks for Time Series Data on Dynamic Graphs

We introduce De Bruijn Graph Neural Networks (DBGNNs), a novel time-aware graph neural network architecture for time-resolved data on dynamic graphs. Our approach accounts for temporal-topological patterns that unfold in the causal topology of dynamic graphs, which is determined by causal walks, i.e. temporally ordered sequences of links by which nodes can influence each other over time. Our architecture builds on multiple layers of higher-order De Bruijn graphs, an iterative line graph construction where nodes in a De Bruijn graph of order k represent walks of length k-1, while edges represent walks of length k. We develop a graph neural network architecture that utilizes De Bruijn graphs to implement a message passing scheme that follows a non-Markovian dynamics, which enables us to learn patterns in the causal topology of a dynamic graph. Addressing the issue that De Bruijn graphs with different orders k can be used to model the same data set, we further apply statistical model selection to determine the optimal graph topology to be used for message passing. An evaluation in synthetic and empirical data sets suggests that DBGNNs can leverage temporal patterns in dynamic graphs, which substantially improves the performance in a supervised node classification task.

Predicting Influential Higher-Order Patterns in Temporal Network Data

Networks are frequently used to model complex systems comprised of interacting elements. While links capture the topology of direct interactions, the true complexity of many systems originates from higher-order patterns in paths by which nodes can indirectly influence each other. Path data, representing ordered sequences of consecutive direct interactions, can be used to model these patterns. However, to avoid overfitting, such models should only consider those higher-order patterns for which the data provide sufficient statistical evidence. On the other hand, we hypothesise that network models, which capture only direct interactions, underfit higher-order patterns present in data. Consequently, both approaches are likely to misidentify influential nodes in complex networks. We contribute to this issue by proposing eight centrality measures based on MOGen, a multi-order generative model that accounts for all paths up to a maximum distance but disregards paths at higher distances. We compare MOGen-based centralities to equivalent measures for network models and path data in a prediction experiment where we aim to identify influential nodes in out-of-sample data. Our results show strong evidence supporting our hypothesis. MOGen consistently outperforms both the network model and path-based prediction. We further show that the performance difference between MOGen and the path-based approach disappears if we have sufficient observations, confirming that the error is due to overfitting.

Higher-Order Visualization of Causal Structures in Dynamics Graphs

Graph drawing and visualisation techniques are important tools for the exploratory analysis of complex systems. While these methods are regularly applied to visualise data on complex networks, we increasingly have access to time series data that can be modelled as temporal networks or dynamic graphs. In such dynamic graphs, the temporal ordering of time-stamped edges determines the causal topology of a system, i.e. which nodes can directly and indirectly influence each other via a so-called causal path. While this causal topology is crucial to understand dynamical processes, the role of nodes, or cluster structures, we lack graph drawing techniques that incorporate this information into static visualisations. Addressing this gap, we present a novel dynamic graph drawing algorithm that utilises higher-order graphical models of causal paths in time series data to compute time-aware static graph visualisations. These visualisations combine the simplicity of static graphs with a time-aware layout algorithm that highlights patterns in the causal topology that result from the temporal dynamics of edges.