Bayesian Detection of Mesoscale Structures in Pathway Data on Graphs

Mesoscale structures are an integral part of the abstraction and analysis of complex systems. They reveal a node's function in the network, and facilitate our understanding of the network dynamics. For example, they can represent communities in social or citation networks, roles in corporate interactions, or core-periphery structures in transportation networks. We usually detect mesoscale structures under the assumption of independence of interactions. Still, in many cases, the interactions invalidate this assumption by occurring in a specific order. Such patterns emerge in pathway data; to capture them, we have to model the dependencies between interactions using higher-order network models. However, the detection of mesoscale structures in higher-order networks is still under-researched. In this work, we derive a Bayesian approach that simultaneously models the optimal partitioning of nodes in groups and the optimal higher-order network dynamics between the groups. In synthetic data we demonstrate that our method can recover both standard proximity-based communities and role-based groupings of nodes. In synthetic and real world data we show that it can compete with baseline techniques, while additionally providing interpretable abstractions of network dynamics.

Bayesian Inference of Transition Matrices from Incomplete Graph Data with a Topological Prior

Many network analysis and graph learning techniques are based on models of random walks which require to infer transition matrices that formalize the underlying stochastic process in an observed graph. For weighted graphs, it is common to estimate the entries of such transition matrices based on the relative weights of edges. However, we are often confronted with incomplete data, which turns the construction of the transition matrix based on a weighted graph into an inference problem. Moreover, we often have access to additional information, which capture topological constraints of the system, i.e. which edges in a weighted graph are (theoretically) possible and which are not, e.g. transportation networks, where we have access to passenger trajectories as well as the physical topology of connections, or a set of social interactions with the underlying social structure. Combining these two different sources of information to infer transition matrices is an open challenge, with implications on the downstream network analysis tasks. Addressing this issue, we show that including knowledge on such topological constraints can improve the inference of transition matrices, especially for small datasets. We derive an analytically tractable Bayesian method that uses repeated interactions and a topological prior to infer transition matrices data-efficiently. We compare it against commonly used frequentist and Bayesian approaches both in synthetic and real-world datasets, and we find that it recovers the transition probabilities with higher accuracy and that it is robust even in cases when the knowledge of the topological constraint is partial. Lastly, we show that this higher accuracy improves the results for downstream network analysis tasks like cluster detection and node ranking, which highlights the practical relevance of our method for analyses of various networked systems.

Inference of time-ordered multibody interactions

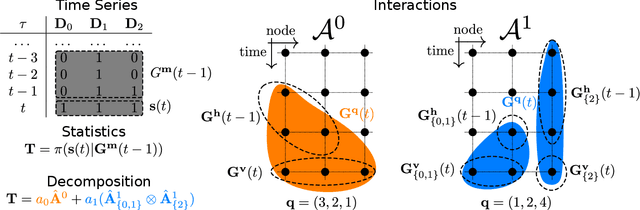
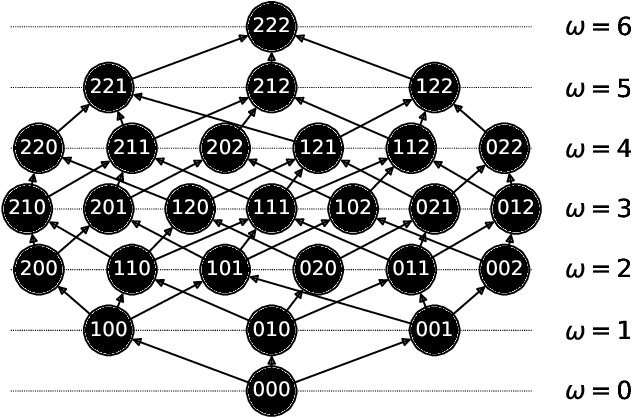
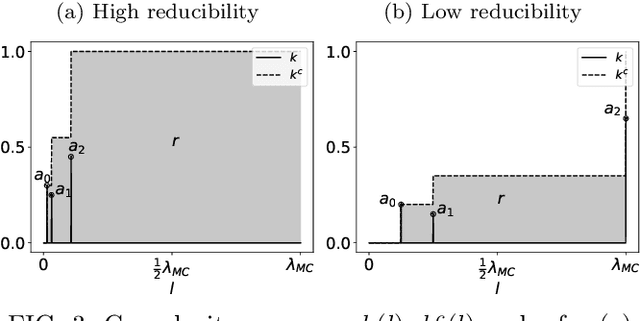
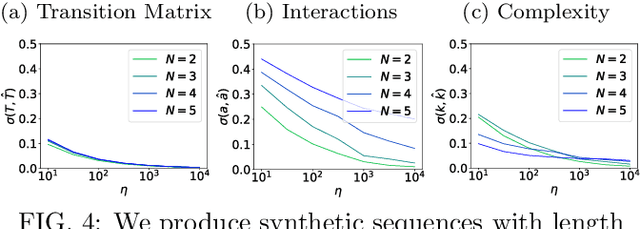
We introduce time-ordered multibody interactions to describe complex systems manifesting temporal as well as multibody dependencies. First, we show how the dynamics of multivariate Markov chains can be decomposed in ensembles of time-ordered multibody interactions. Then, we present an algorithm to extract combined interactions from data and a measure to characterize the complexity of interaction ensembles. Finally, we experimentally validate the robustness of our algorithm against statistical errors and its efficiency at obtaining simple interaction ensembles.

Learning the Markov order of paths in a network

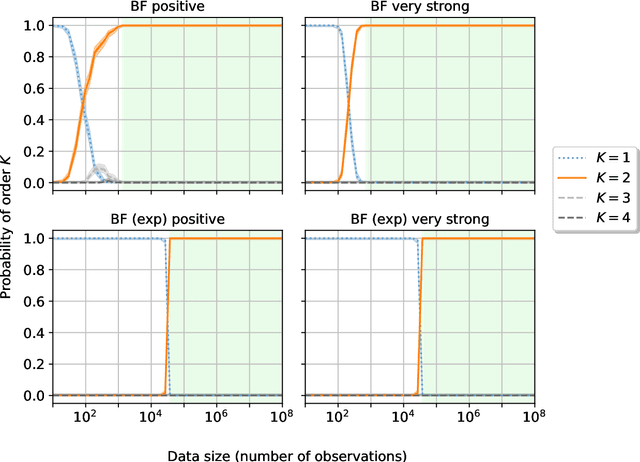
We study the problem of learning the Markov order in categorical sequences that represent paths in a network, i.e. sequences of variable lengths where transitions between states are constrained to a known graph. Such data pose challenges for standard Markov order detection methods and demand modelling techniques that explicitly account for the graph constraint. Adopting a multi-order modelling framework for paths, we develop a Bayesian learning technique that (i) more reliably detects the correct Markov order compared to a competing method based on the likelihood ratio test, (ii) requires considerably less data compared to methods using AIC or BIC, and (iii) is robust against partial knowledge of the underlying constraints. We further show that a recently published method that uses a likelihood ratio test has a tendency to overfit the true Markov order of paths, which is not the case for our Bayesian technique. Our method is important for data scientists analyzing patterns in categorical sequence data that are subject to (partially) known constraints, e.g. sequences with forbidden words, mobility trajectories and click stream data, or sequence data in bioinformatics. Addressing the key challenge of model selection, our work is further relevant for the growing body of research that emphasizes the need for higher-order models in network analysis.