From Specifications to Behavior: Maneuver Verification in a Semantic State Space

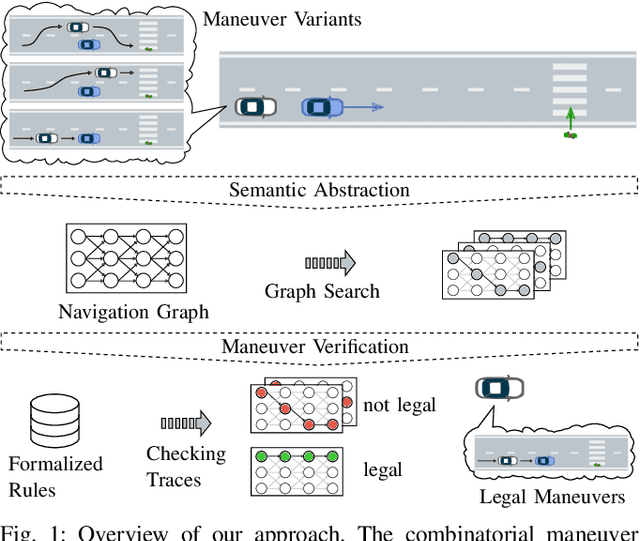
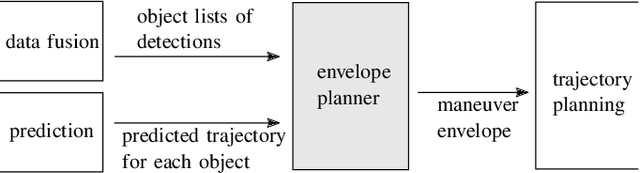
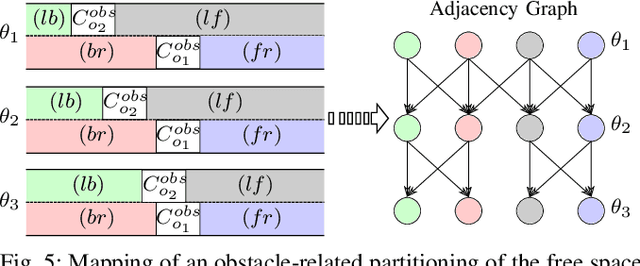
To realize a market entry of autonomous vehicles in the foreseeable future, the behavior planning system will need to abide by the same rules that humans follow. Product liability cannot be enforced without a proper solution to the approval trap. In this paper, we define a semantic abstraction of the continuous space and formalize traffic rules in linear temporal logic (LTL). Sequences in the semantic state space represent maneuvers a high-level planner could choose to execute. We check these maneuvers against the formalized traffic rules using runtime verification. By using the standard model checker NuSMV, we demonstrate the effectiveness of our approach and provide runtime properties for the maneuver verification. We show that high-level behavior can be verified in a semantic state space to fulfill a set of formalized rules, which could serve as a step towards safety of the intended functionality.

The Simpler the Better: Constant Velocity for Pedestrian Motion Prediction

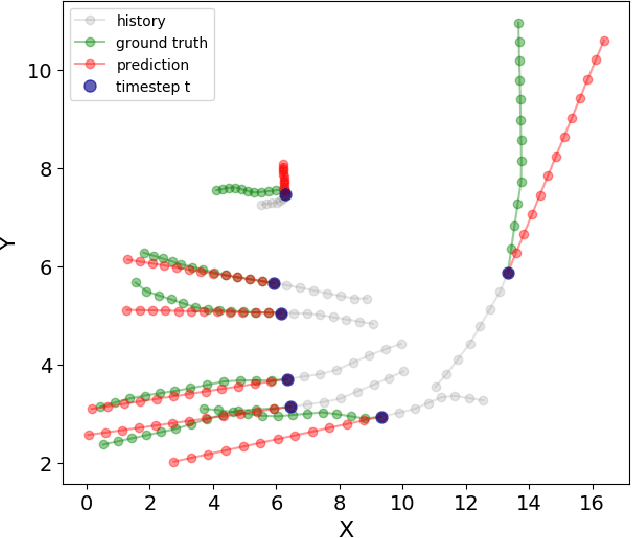
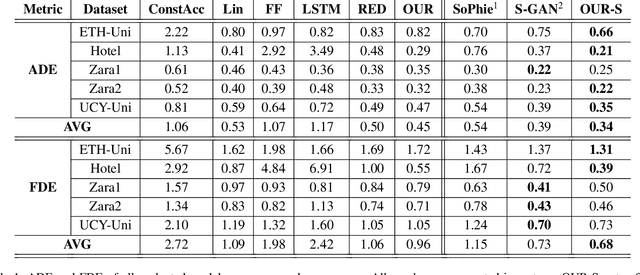
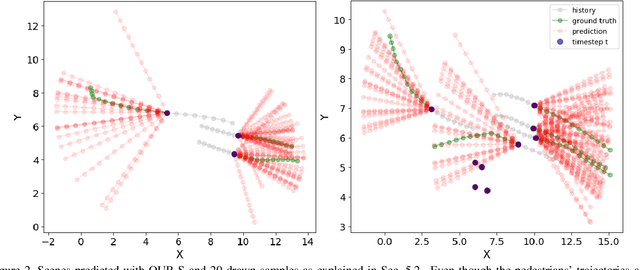
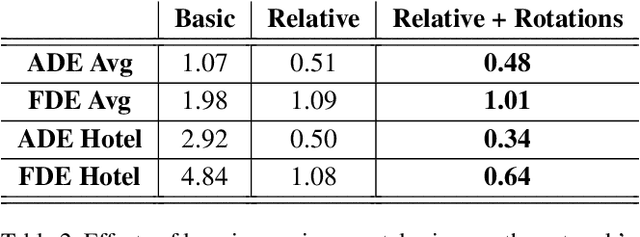
Pedestrian motion prediction is a fundamental task for autonomous robots and vehicles to operate safely. In recent years many complex models have been proposed to address this problem. While complex models can be justified, simple models should be preferred given the same or better performance. In this work we show that a simple Constant Velocity Model can achieve competitive performance on this task. We evaluate the Constant Velocity Model using two popular benchmark datasets for pedestrian motion prediction and show that it outperforms state-of-the-art models and several common baselines. The success of this model indicates that either neural networks are not able to make use of the additional information they are provided with, or it is not as relevant as commonly believed. Therefore, we analyze how neural networks process this information and how it impacts their predictions. Our analysis shows that neural networks implicitly learn environmental priors that have a negative impact on their generalization capability, most of the pedestrian's motion history is ignored and interactions - while happening - are too complex to predict. These findings explain the success of the Constant Velocity Model and lead to a better understanding of the problem at hand.

Traceability of Deep Neural Networks

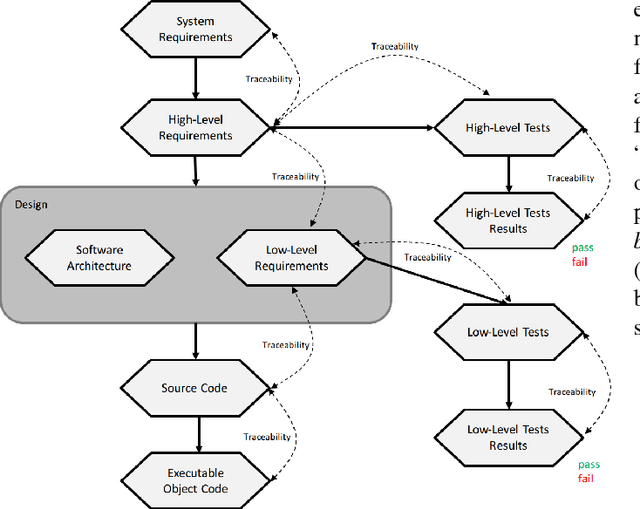
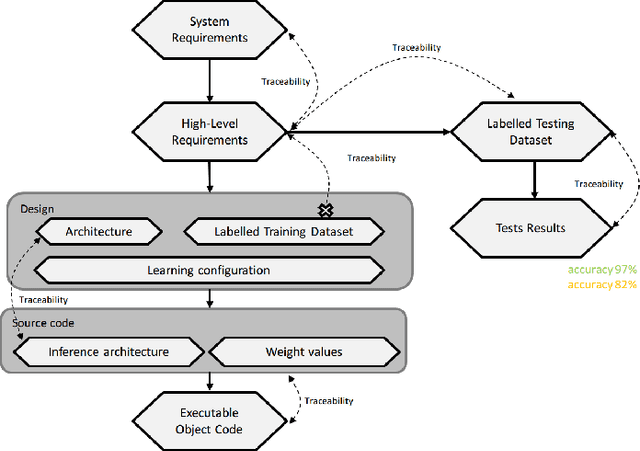
[Context.] The success of deep learning makes its usage more and more tempting in safety-critical applications. However such applications have historical standards (e.g., DO178, ISO26262) which typically do not envision the usage of machine learning. We focus in particular on \emph{requirements traceability} of software artifacts, i.e., code modules, functions, or statements (depending on the desired granularity). [Problem.] Both code and requirements are a problem when dealing with deep neural networks: code constituting the network is not comparable to classical code; furthermore, requirements for applications where neural networks are required are typically very hard to specify: even though high-level requirements can be defined, it is very hard to make such requirements concrete enough, that one can qualify them of low-level requirements. An additional problem is that deep learning is in practice very much based on trial-and-error, which makes the final result hard to explain without the previous iterations. [Proposed solution.] We investigate which artifacts could play a similar role to code or low-level requirements in neural network development and propose various traces which one could possibly consider as a replacement for classical notions. We also propose a form of traceability (and new artifacts) in order to deal with the particular trial-and-error development process for deep learning.

Decidability and Undecidability Results for Propositional Schemata

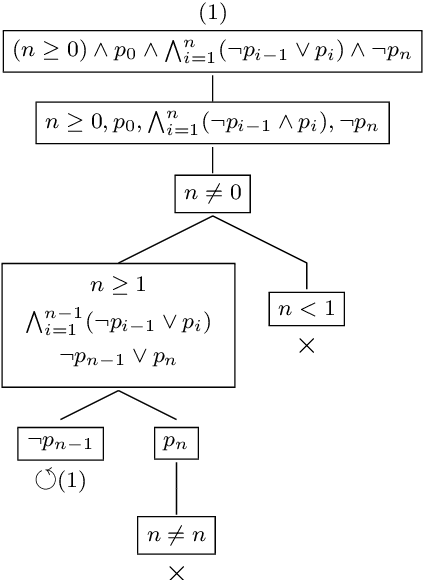
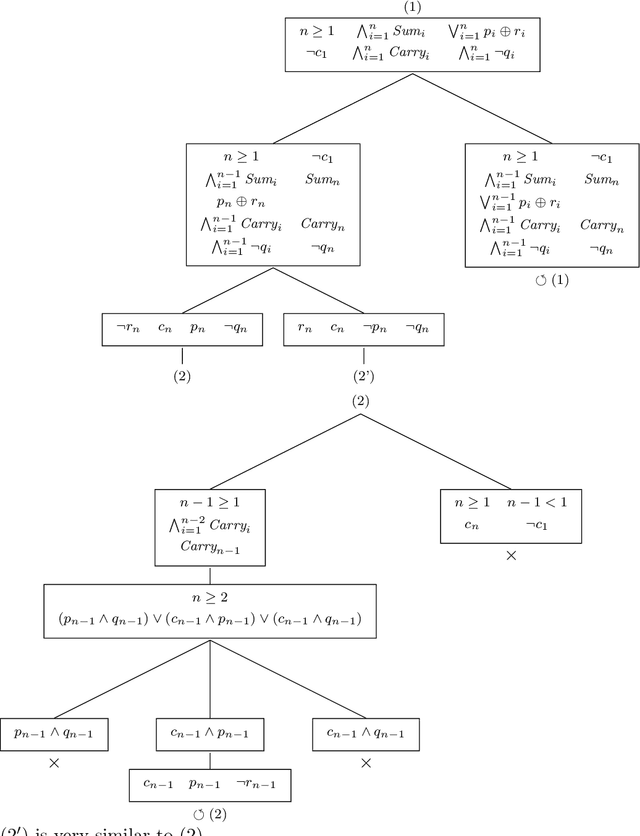
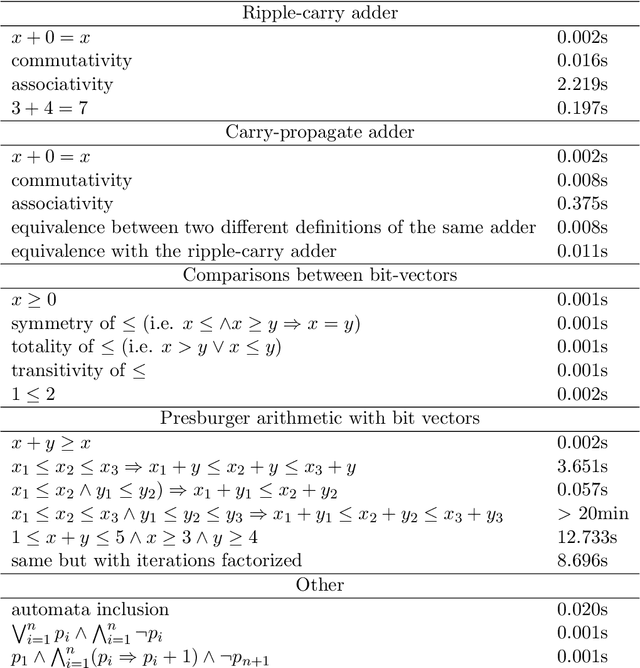
We define a logic of propositional formula schemata adding to the syntax of propositional logic indexed propositions and iterated connectives ranging over intervals parameterized by arithmetic variables. The satisfiability problem is shown to be undecidable for this new logic, but we introduce a very general class of schemata, called bound-linear, for which this problem becomes decidable. This result is obtained by reduction to a particular class of schemata called regular, for which we provide a sound and complete terminating proof procedure. This schemata calculus allows one to capture proof patterns corresponding to a large class of problems specified in propositional logic. We also show that the satisfiability problem becomes again undecidable for slight extensions of this class, thus demonstrating that bound-linear schemata represent a good compromise between expressivity and decidability.

Generating Schemata of Resolution Proofs

Two distinct algorithms are presented to extract (schemata of) resolution proofs from closed tableaux for propositional schemata. The first one handles the most efficient version of the tableau calculus but generates very complex derivations (denoted by rather elaborate rewrite systems). The second one has the advantage that much simpler systems can be obtained, however the considered proof procedure is less efficient.

Linear Temporal Logic and Propositional Schemata, Back and Forth (extended version)

This paper relates the well-known Linear Temporal Logic with the logic of propositional schemata introduced by the authors. We prove that LTL is equivalent to a class of schemata in the sense that polynomial-time reductions exist from one logic to the other. Some consequences about complexity are given. We report about first experiments and the consequences about possible improvements in existing implementations are analyzed.

A Decidable Class of Nested Iterated Schemata

Many problems can be specified by patterns of propositional formulae depending on a parameter, e.g. the specification of a circuit usually depends on the number of bits of its input. We define a logic whose formulae, called "iterated schemata", allow to express such patterns. Schemata extend propositional logic with indexed propositions, e.g. P_i, P_i+1, P_1, and with generalized connectives, e.g. /\i=1..n or i=1..n (called "iterations") where n is an (unbound) integer variable called a "parameter". The expressive power of iterated schemata is strictly greater than propositional logic: it is even out of the scope of first-order logic. We define a proof procedure, called DPLL*, that can prove that a schema is satisfiable for at least one value of its parameter, in the spirit of the DPLL procedure. However the converse problem, i.e. proving that a schema is unsatisfiable for every value of the parameter, is undecidable so DPLL* does not terminate in general. Still, we prove that it terminates for schemata of a syntactic subclass called "regularly nested". This is the first non trivial class for which DPLL* is proved to terminate. Furthermore the class of regularly nested schemata is the first decidable class to allow nesting of iterations, i.e. to allow schemata of the form /\i=1..n (/\j=1..n ...).