Decidability and Undecidability Results for Propositional Schemata

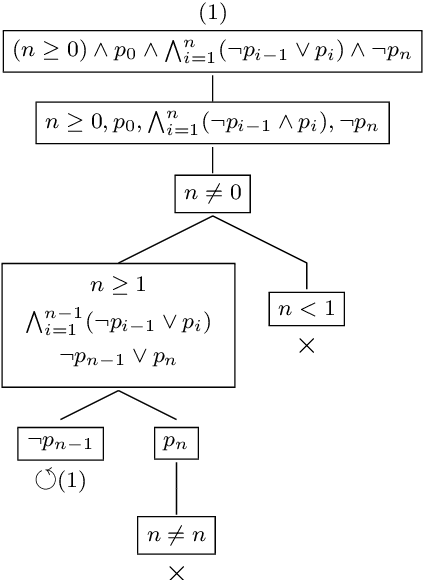
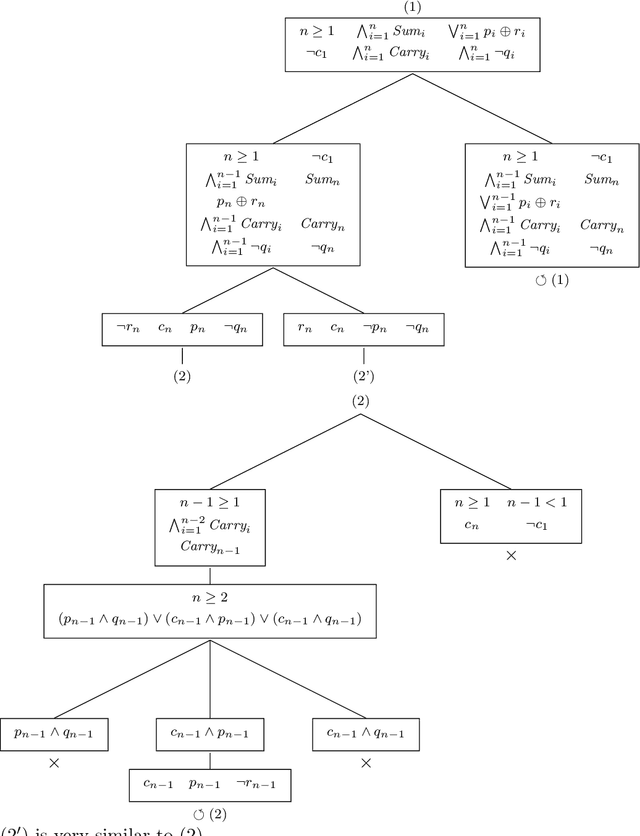
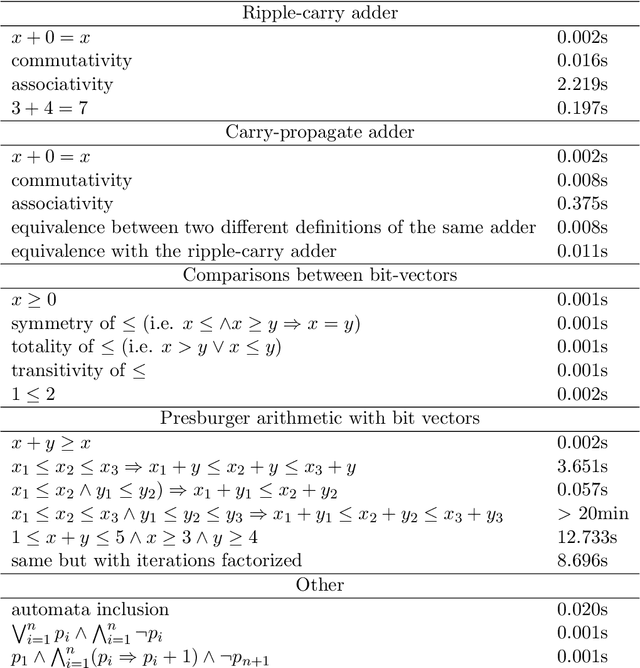
We define a logic of propositional formula schemata adding to the syntax of propositional logic indexed propositions and iterated connectives ranging over intervals parameterized by arithmetic variables. The satisfiability problem is shown to be undecidable for this new logic, but we introduce a very general class of schemata, called bound-linear, for which this problem becomes decidable. This result is obtained by reduction to a particular class of schemata called regular, for which we provide a sound and complete terminating proof procedure. This schemata calculus allows one to capture proof patterns corresponding to a large class of problems specified in propositional logic. We also show that the satisfiability problem becomes again undecidable for slight extensions of this class, thus demonstrating that bound-linear schemata represent a good compromise between expressivity and decidability.

Linear Temporal Logic and Propositional Schemata, Back and Forth (extended version)

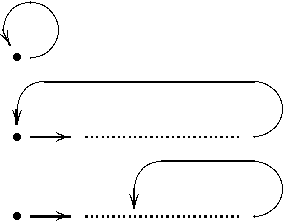
This paper relates the well-known Linear Temporal Logic with the logic of propositional schemata introduced by the authors. We prove that LTL is equivalent to a class of schemata in the sense that polynomial-time reductions exist from one logic to the other. Some consequences about complexity are given. We report about first experiments and the consequences about possible improvements in existing implementations are analyzed.

A Decidable Class of Nested Iterated Schemata

Many problems can be specified by patterns of propositional formulae depending on a parameter, e.g. the specification of a circuit usually depends on the number of bits of its input. We define a logic whose formulae, called "iterated schemata", allow to express such patterns. Schemata extend propositional logic with indexed propositions, e.g. P_i, P_i+1, P_1, and with generalized connectives, e.g. /\i=1..n or i=1..n (called "iterations") where n is an (unbound) integer variable called a "parameter". The expressive power of iterated schemata is strictly greater than propositional logic: it is even out of the scope of first-order logic. We define a proof procedure, called DPLL*, that can prove that a schema is satisfiable for at least one value of its parameter, in the spirit of the DPLL procedure. However the converse problem, i.e. proving that a schema is unsatisfiable for every value of the parameter, is undecidable so DPLL* does not terminate in general. Still, we prove that it terminates for schemata of a syntactic subclass called "regularly nested". This is the first non trivial class for which DPLL* is proved to terminate. Furthermore the class of regularly nested schemata is the first decidable class to allow nesting of iterations, i.e. to allow schemata of the form /\i=1..n (/\j=1..n ...).