Generalization error bounds for DECONET: a deep unfolding network for analysis Compressive Sensing

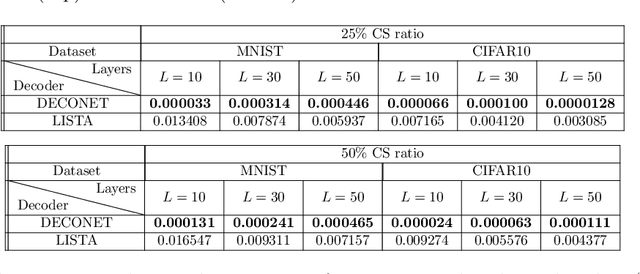
In this paper, we propose a new deep unfolding neural network -- based on a state-of-the-art optimization algorithm -- for analysis Compressed Sensing. The proposed network called Decoding Network (DECONET) implements a decoder that reconstructs vectors from their incomplete, noisy measurements. Moreover, DECONET jointly learns a redundant analysis operator for sparsification, which is shared across the layers of DECONET. We study the generalization ability of DECONET. Towards that end, we first estimate the Rademacher complexity of the hypothesis class consisting of all the decoders that DECONET can implement. Then, we provide generalization error bounds, in terms of the aforementioned estimate. Finally, we present numerical experiments which confirm the validity of our theoretical results.

Spark Deficient Gabor Frames for Inverse Problems

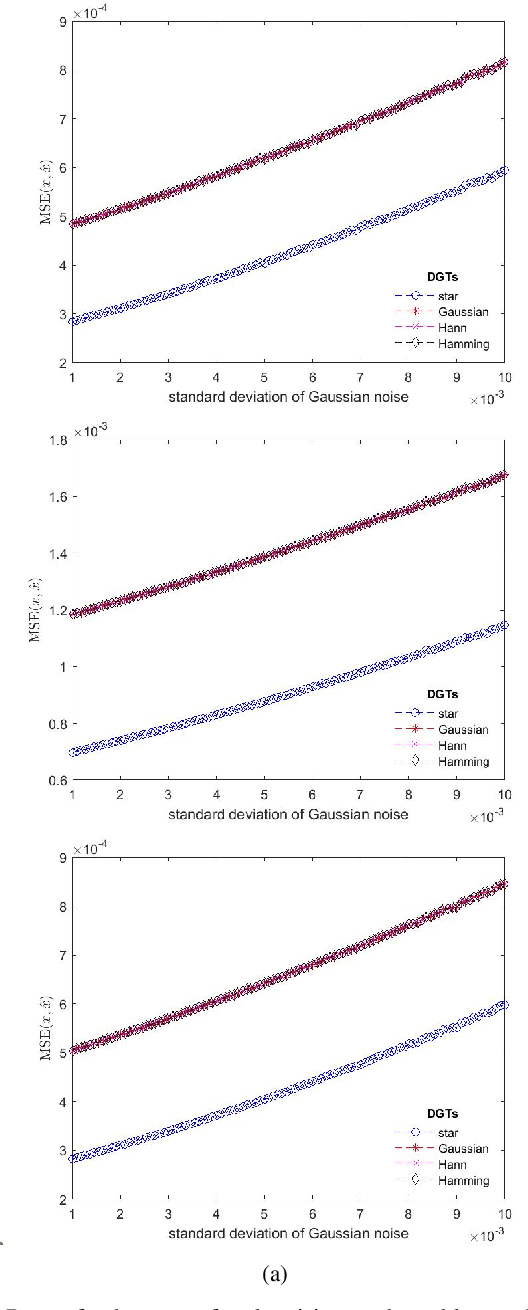
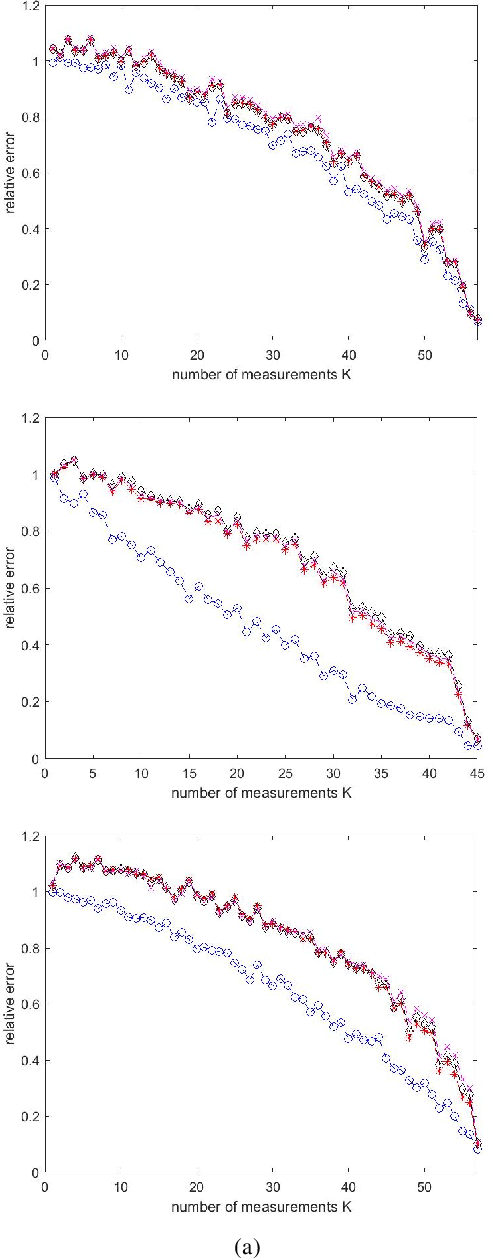
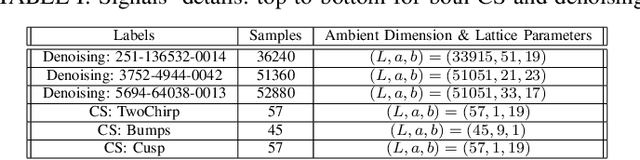
In this paper, we apply star-Digital Gabor Transform in analysis Compressed Sensing and speech denoising. Based on assumptions on the ambient dimension, we produce a window vector that generates a spark deficient Gabor frame with many linear dependencies among its elements. We conduct computational experiments on both synthetic and real-world signals, using as baseline three Gabor transforms generated by state-of-the-art window vectors and compare their performance to star-Gabor transform. Results show that the proposed star-Gabor transform outperforms all others in all signal cases.

ADMM-DAD net: a deep unfolding network for analysis compressed sensing

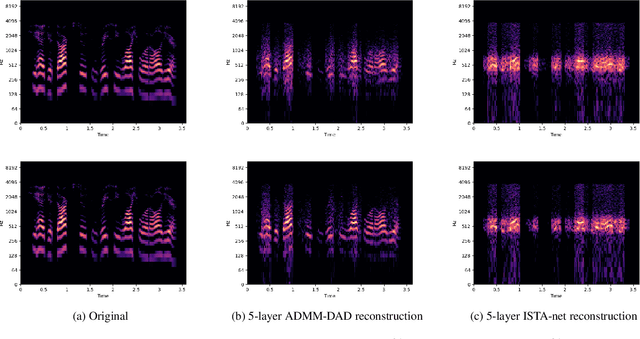
In this paper, we propose a new deep unfolding neural network based on the ADMM algorithm for analysis Compressed Sensing. The proposed network jointly learns a redundant analysis operator for sparsification and reconstructs the signal of interest. We compare our proposed network with a state-of-the-art unfolded ISTA decoder, that also learns an orthogonal sparsifier. Moreover, we consider not only image, but also speech datasets as test examples. Computational experiments demonstrate that our proposed network outperforms the state-of-the-art deep unfolding networks, consistently for both real-world image and speech datasets.

Star DGT: a Robust Gabor Transform for Speech Denoising

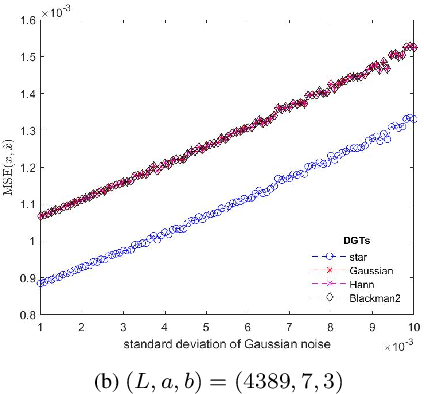
In this paper, we address the speech denoising problem, where white Gaussian additive noise is to be removed from a given speech signal. Our approach is based on a redundant, analysis-sparse representation of the original speech signal. We pick an eigenvector of the Zauner unitary matrix and -- under certain assumptions on the ambient dimension -- we use it as window vector to generate a spark deficient Gabor frame. The analysis operator associated with such a frame, is a (highly) redundant Gabor transform, which we use as a sparsifying transform in denoising procedure. We conduct computational experiments on real-world speech data, solving the analysis basis pursuit denoising problem, with four different choices of analysis operators, including our Gabor analysis operator. The results show that our proposed redundant Gabor transform outperforms -- in all cases -- Gabor transforms generated by state-of-the-art window vectors of time-frequency analysis.