Star DGT: a Robust Gabor Transform for Speech Denoising

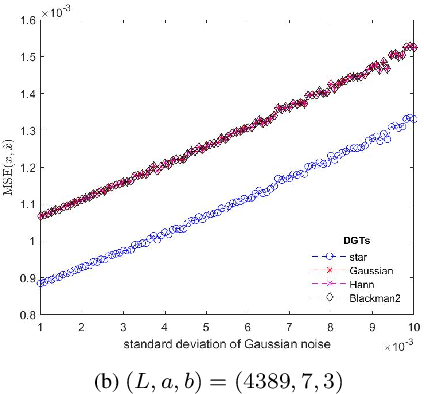
In this paper, we address the speech denoising problem, where white Gaussian additive noise is to be removed from a given speech signal. Our approach is based on a redundant, analysis-sparse representation of the original speech signal. We pick an eigenvector of the Zauner unitary matrix and -- under certain assumptions on the ambient dimension -- we use it as window vector to generate a spark deficient Gabor frame. The analysis operator associated with such a frame, is a (highly) redundant Gabor transform, which we use as a sparsifying transform in denoising procedure. We conduct computational experiments on real-world speech data, solving the analysis basis pursuit denoising problem, with four different choices of analysis operators, including our Gabor analysis operator. The results show that our proposed redundant Gabor transform outperforms -- in all cases -- Gabor transforms generated by state-of-the-art window vectors of time-frequency analysis.