Generalization error bounds for DECONET: a deep unfolding network for analysis Compressive Sensing
Paper and Code
May 21, 2022
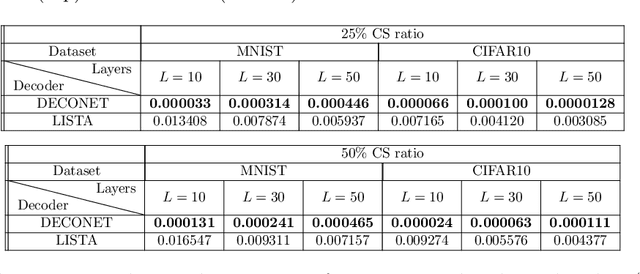

In this paper, we propose a new deep unfolding neural network -- based on a state-of-the-art optimization algorithm -- for analysis Compressed Sensing. The proposed network called Decoding Network (DECONET) implements a decoder that reconstructs vectors from their incomplete, noisy measurements. Moreover, DECONET jointly learns a redundant analysis operator for sparsification, which is shared across the layers of DECONET. We study the generalization ability of DECONET. Towards that end, we first estimate the Rademacher complexity of the hypothesis class consisting of all the decoders that DECONET can implement. Then, we provide generalization error bounds, in terms of the aforementioned estimate. Finally, we present numerical experiments which confirm the validity of our theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge