D3: Data Diversity Design for Systematic Generalization in Visual Question Answering

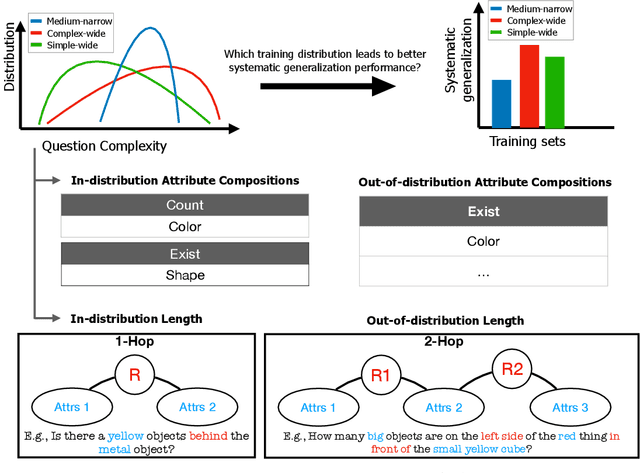
Systematic generalization is a crucial aspect of intelligence, which refers to the ability to generalize to novel tasks by combining known subtasks and concepts. One critical factor that has been shown to influence systematic generalization is the diversity of training data. However, diversity can be defined in various ways, as data have many factors of variation. A more granular understanding of how different aspects of data diversity affect systematic generalization is lacking. We present new evidence in the problem of Visual Question Answering (VQA) that reveals that the diversity of simple tasks (i.e. tasks formed by a few subtasks and concepts) plays a key role in achieving systematic generalization. This implies that it may not be essential to gather a large and varied number of complex tasks, which could be costly to obtain. We demonstrate that this result is independent of the similarity between the training and testing data and applies to well-known families of neural network architectures for VQA (i.e. monolithic architectures and neural module networks). Additionally, we observe that neural module networks leverage all forms of data diversity we evaluated, while monolithic architectures require more extensive amounts of data to do so. These findings provide a first step towards understanding the interactions between data diversity design, neural network architectures, and systematic generalization capabilities.

Transformer Module Networks for Systematic Generalization in Visual Question Answering

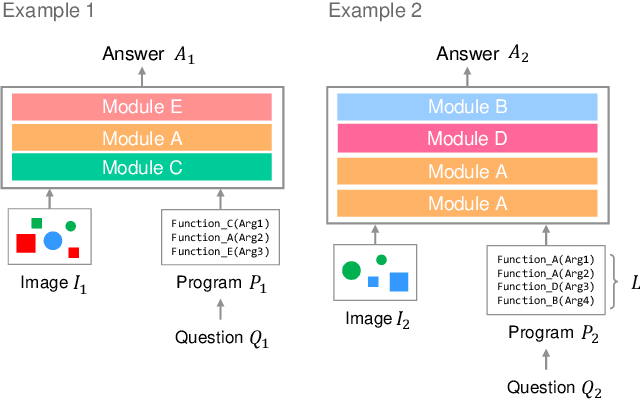
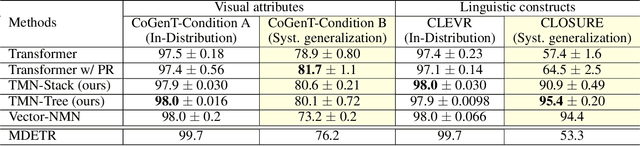
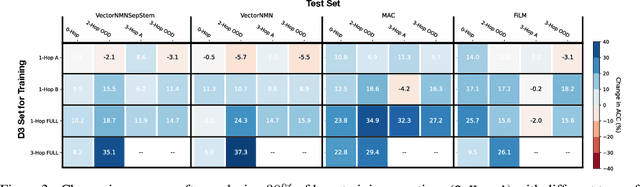
Transformer-based models achieve great performance on Visual Question Answering (VQA). However, when we evaluate them on systematic generalization, i.e., handling novel combinations of known concepts, their performance degrades. Neural Module Networks (NMNs) are a promising approach for systematic generalization that consists on composing modules, i.e., neural networks that tackle a sub-task. Inspired by Transformers and NMNs, we propose Transformer Module Network (TMN), a novel Transformer-based model for VQA that dynamically composes modules into a question-specific Transformer network. TMNs achieve state-of-the-art systematic generalization performance in three VQA datasets, namely, CLEVR-CoGenT, CLOSURE and GQA-SGL, in some cases improving more than 30% over standard Transformers.

The Foes of Neural Network's Data Efficiency Among Unnecessary Input Dimensions

Datasets often contain input dimensions that are unnecessary to predict the output label, e.g. background in object recognition, which lead to more trainable parameters. Deep Neural Networks (DNNs) are robust to increasing the number of parameters in the hidden layers, but it is unclear whether this holds true for the input layer. In this letter, we investigate the impact of unnecessary input dimensions on a central issue of DNNs: their data efficiency, ie. the amount of examples needed to achieve certain generalization performance. Our results show that unnecessary input dimensions that are task-unrelated substantially degrade data efficiency. This highlights the need for mechanisms that remove {task-unrelated} dimensions to enable data efficiency gains.

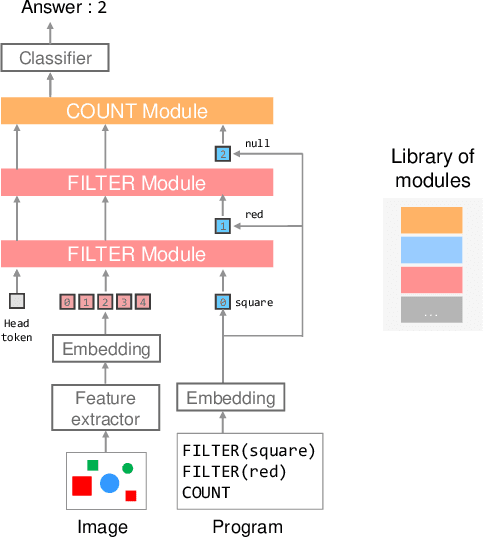
How Modular Should Neural Module Networks Be for Systematic Generalization?

Neural Module Networks (NMNs) aim at Visual Question Answering (VQA) via composition of modules that tackle a sub-task. NMNs are a promising strategy to achieve systematic generalization, i.e. overcoming biasing factors in the training distribution. However, the aspects of NMNs that facilitate systematic generalization are not fully understood. In this paper, we demonstrate that the stage and the degree at which modularity is defined has large influence on systematic generalization. In a series of experiments on three VQA datasets (MNIST with multiple attributes, SQOOP, and CLEVR-CoGenT), our results reveal that tuning the degree of modularity in the network, especially at the image encoder stage, reaches substantially higher systematic generalization. These findings lead to new NMN architectures that outperform previous ones in terms of systematic generalization.

Removable and/or Repeated Units Emerge in Overparametrized Deep Neural Networks

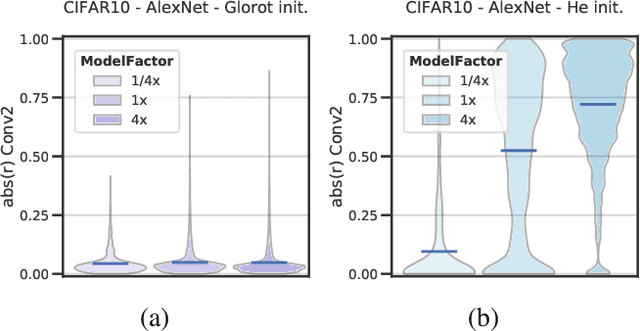
Deep neural networks (DNNs) perform well on a variety of tasks despite the fact that most networks used in practice are vastly overparametrized and even capable of perfectly fitting randomly labeled data. Recent evidence suggests that developing compressible representations is key for adjusting the complexity of overparametrized networks to the task at hand. In this paper, we provide new empirical evidence that supports this hypothesis by identifying two types of units that emerge when the network's width is increased: removable units which can be dropped out of the network without significant change to the output and repeated units whose activities are highly correlated with other units. The emergence of these units implies capacity constraints as the function the network represents could be expressed by a smaller network without these units. In a series of experiments with AlexNet, ResNet and Inception networks in the CIFAR-10 and ImageNet datasets, and also using shallow networks with synthetic data, we show that DNNs consistently increase either the number of removable units, repeated units, or both at greater widths for a comprehensive set of hyperparameters. These results suggest that the mechanisms by which networks in the deep learning regime adjust their complexity operate at the unit level and highlight the need for additional research into what drives the emergence of such units.