Information Planning for Text Data

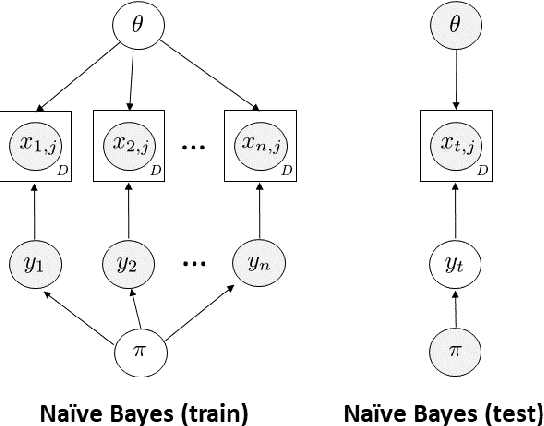
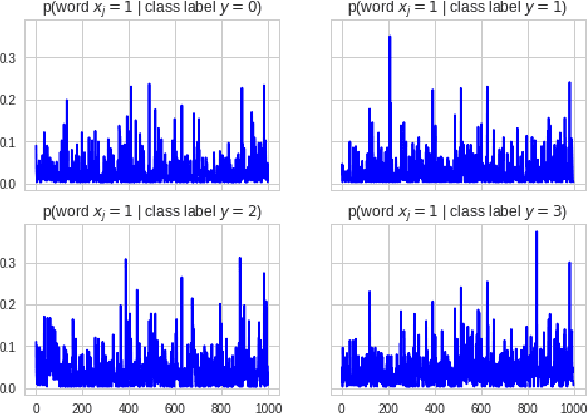
Information planning enables faster learning with fewer training examples. It is particularly applicable when training examples are costly to obtain. This work examines the advantages of information planning for text data by focusing on three supervised models: Naive Bayes, supervised LDA and deep neural networks. We show that planning based on entropy and mutual information outperforms random selection baseline and therefore accelerates learning.

Bayesian Nonparametric Modeling of Driver Behavior using HDP Split-Merge Sampling Algorithm

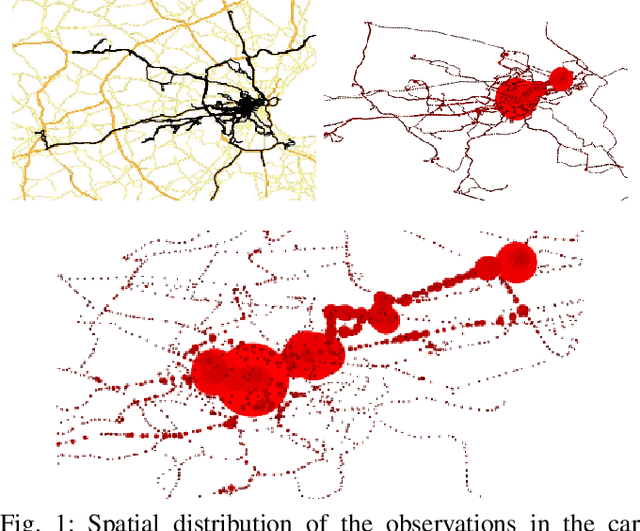
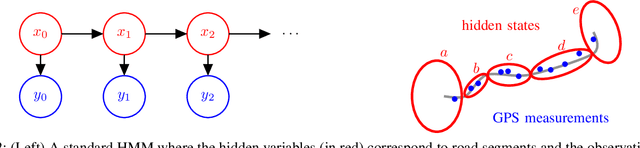
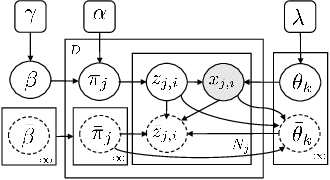
Modern vehicles are equipped with increasingly complex sensors. These sensors generate large volumes of data that provide opportunities for modeling and analysis. Here, we are interested in exploiting this data to learn aspects of behaviors and the road network associated with individual drivers. Our dataset is collected on a standard vehicle used to commute to work and for personal trips. A Hidden Markov Model (HMM) trained on the GPS position and orientation data is utilized to compress the large amount of position information into a small amount of road segment states. Each state has a set of observations, i.e. car signals, associated with it that are quantized and modeled as draws from a Hierarchical Dirichlet Process (HDP). The inference for the topic distributions is carried out using HDP split-merge sampling algorithm. The topic distributions over joint quantized car signals characterize the driving situation in the respective road state. In a novel manner, we demonstrate how the sparsity of the personal road network of a driver in conjunction with a hierarchical topic model allows data driven predictions about destinations as well as likely road conditions.

Adaptive Scan Gibbs Sampler for Large Scale Inference Problems

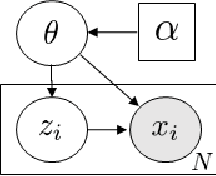
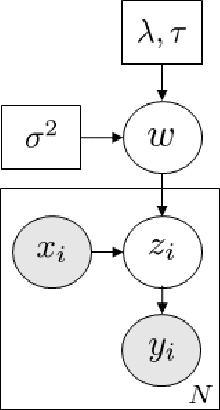
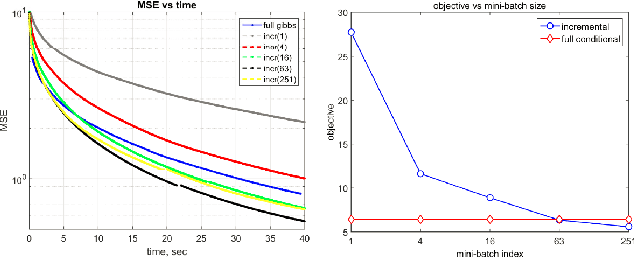
For large scale on-line inference problems the update strategy is critical for performance. We derive an adaptive scan Gibbs sampler that optimizes the update frequency by selecting an optimum mini-batch size. We demonstrate performance of our adaptive batch-size Gibbs sampler by comparing it against the collapsed Gibbs sampler for Bayesian Lasso, Dirichlet Process Mixture Models (DPMM) and Latent Dirichlet Allocation (LDA) graphical models.