Learned 3D volumetric recovery of clouds and its uncertainty for climate analysis

Significant uncertainty in climate prediction and cloud physics is tied to observational gaps relating to shallow scattered clouds. Addressing these challenges requires remote sensing of their three-dimensional (3D) heterogeneous volumetric scattering content. This calls for passive scattering computed tomography (CT). We design a learning-based model (ProbCT) to achieve CT of such clouds, based on noisy multi-view spaceborne images. ProbCT infers - for the first time - the posterior probability distribution of the heterogeneous extinction coefficient, per 3D location. This yields arbitrary valuable statistics, e.g., the 3D field of the most probable extinction and its uncertainty. ProbCT uses a neural-field representation, making essentially real-time inference. ProbCT undergoes supervised training by a new labeled multi-class database of physics-based volumetric fields of clouds and their corresponding images. To improve out-of-distribution inference, we incorporate self-supervised learning through differential rendering. We demonstrate the approach in simulations and on real-world data, and indicate the relevance of 3D recovery and uncertainty to precipitation and renewable energy.

Advances in 3D scattering tomography of cloud micro-physics

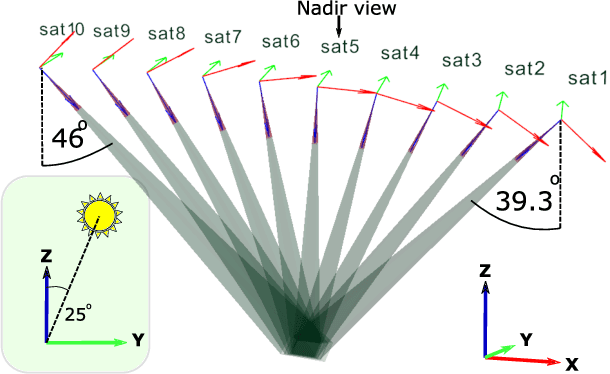
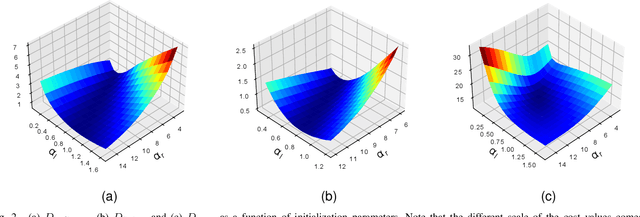
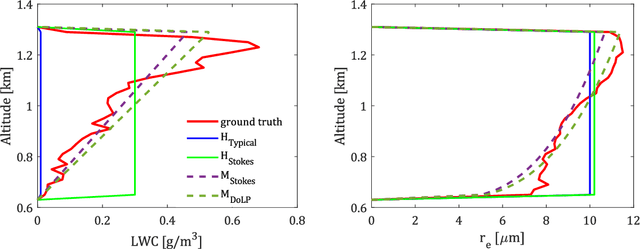
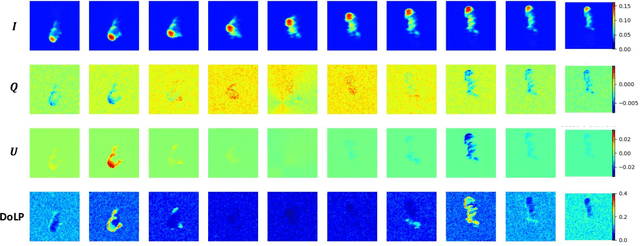
We introduce new adjustments and advances in space-borne 3D volumetric scattering-tomography of cloud micro-physics. The micro-physical properties retrieved are the liquid water content and effective radius within a cloud. New adjustments include an advanced perspective polarization imager model, and the assumption of 3D variation of the effective radius. Under these assumptions, we advanced the retrieval to yield results that (compared to the simulated ground-truth) have smaller errors than the prior art. Elements of our advancement include initialization by a parametric horizontally-uniform micro-physical model. The parameters of this initialization are determined by a grid search of the cost function. Furthermore, we added viewpoints corresponding to single-scattering angles, where polarization yields enhanced sensitivity to the droplet micro-physics (i.e., the cloudbow region). In addition, we introduce an optional adjustment, in which optimization of the liquid water content and effective radius are separated to alternating periods. The suggested initialization model and additional advances have been evaluated by retrieval of a set of large-eddy simulation clouds.

3D Scattering Tomography by Deep Learning with Architecture Tailored to Cloud Fields

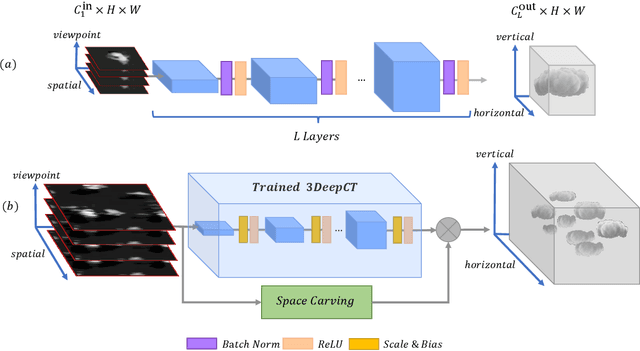
We present 3DeepCT, a deep neural network for computed tomography, which performs 3D reconstruction of scattering volumes from multi-view images. Our architecture is dictated by the stationary nature of atmospheric cloud fields. The task of volumetric scattering tomography aims at recovering a volume from its 2D projections. This problem has been studied extensively, leading, to diverse inverse methods based on signal processing and physics models. However, such techniques are typically iterative, exhibiting high computational load and long convergence time. We show that 3DeepCT outperforms physics-based inverse scattering methods in term of accuracy as well as offering a significant orders of magnitude improvement in computational time. To further improve the recovery accuracy, we introduce a hybrid model that combines 3DeepCT and physics-based method. The resultant hybrid technique enjoys fast inference time and improved recovery performance.

In-situ multi-scattering tomography

To recover the three dimensional (3D) volumetric distribution of matter in an object, images of the object are captured from multiple directions and locations. Using these images tomographic computations extract the distribution. In highly scattering media and constrained, natural irradiance, tomography must explicitly account for off-axis scattering. Furthermore, the tomographic model and recovery must function when imaging is done in-situ, as occurs in medical imaging and ground-based atmospheric sensing. We formulate tomography that handles arbitrary orders of scattering, using a monte-carlo model. Moreover, the model is highly parallelizable in our formulation. This enables large scale rendering and recovery of volumetric scenes having a large number of variables. We solve stability and conditioning problems that stem from radiative transfer (RT) modeling in-situ.