DeepTopPush: Simple and Scalable Method for Accuracy at the Top

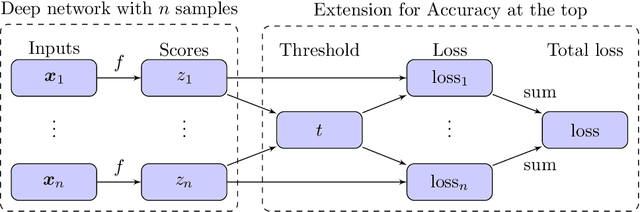
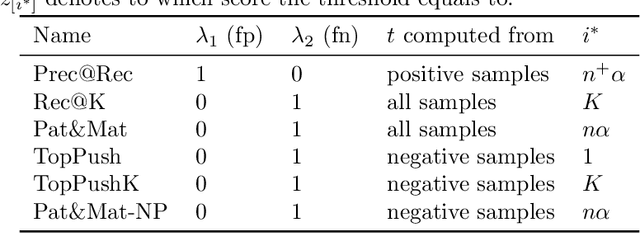
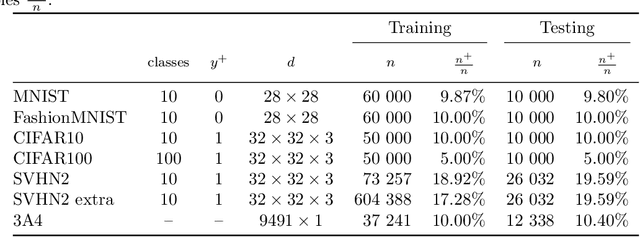
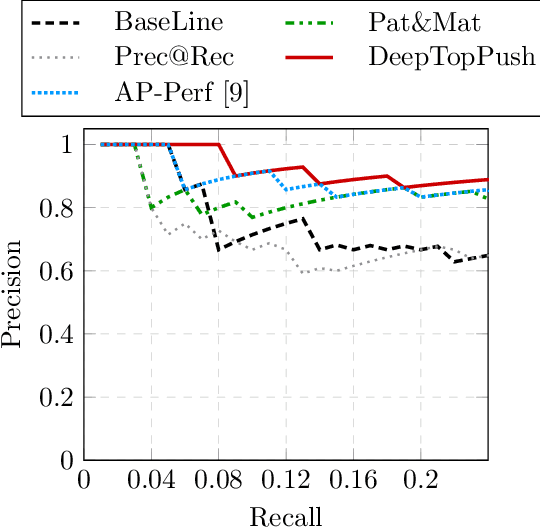
Accuracy at the top is a special class of binary classification problems where the performance is evaluated only on a small number of relevant (top) samples. Applications include information retrieval systems or processes with manual (expensive) postprocessing. This leads to the minimization of irrelevant samples above a threshold. We consider classifiers in the form of an arbitrary (deep) network and propose a new method DeepTopPush for minimizing the top loss function. Since the threshold depends on all samples, the problem is non-decomposable. We modify the stochastic gradient descent to handle the non-decomposability in an end-to-end training manner and propose a way to estimate the threshold only from values on the current minibatch. We demonstrate the good performance of DeepTopPush on visual recognition datasets and on a real-world application of selecting a small number of molecules for further drug testing.

Nonlinear classifiers for ranking problems based on kernelized SVM

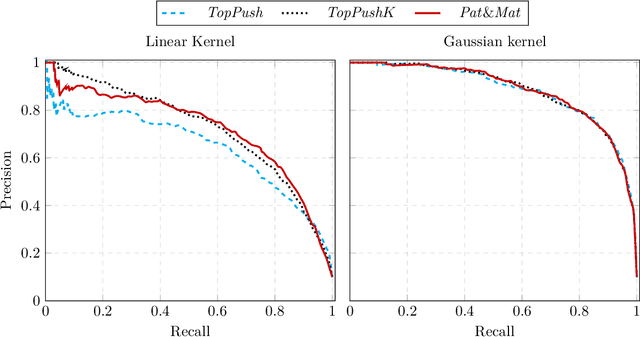
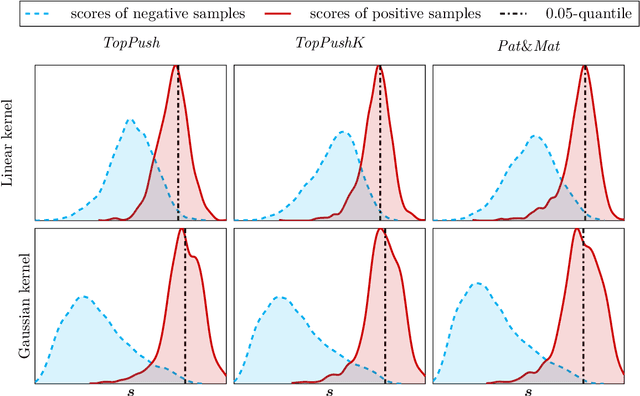
Many classification problems focus on maximizing the performance only on the samples with the highest relevance instead of all samples. As an example, we can mention ranking problems, accuracy at the top or search engines where only the top few queries matter. In our previous work, we derived a general framework including several classes of these linear classification problems. In this paper, we extend the framework to nonlinear classifiers. Utilizing a similarity to SVM, we dualize the problems, add kernels and propose a componentwise dual ascent method. This allows us to perform one iteration in less than 20 milliseconds on relatively large datasets such as FashionMNIST.

General Framework for Binary Classification on Top Samples

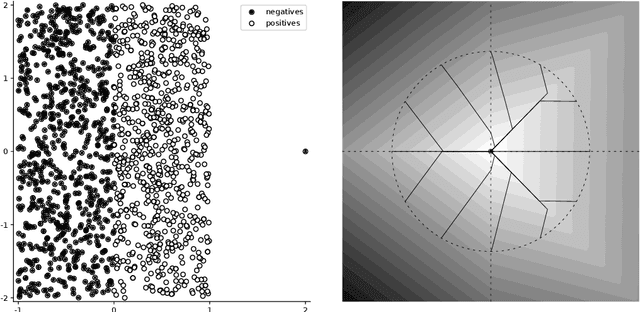
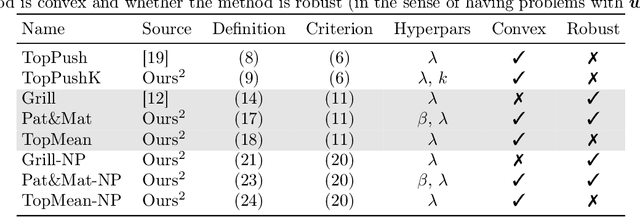
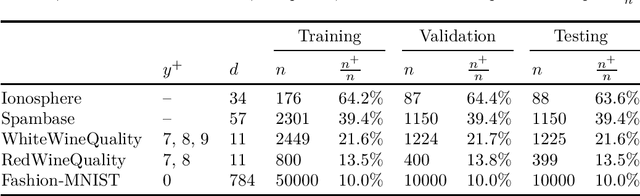
Many binary classification problems minimize misclassification above (or below) a threshold. We show that instances of ranking problems, accuracy at the top or hypothesis testing may be written in this form. We propose a general framework to handle these classes of problems and show which known methods (both known and newly proposed) fall into this framework. We provide a theoretical analysis of this framework and mention selected possible pitfalls the methods may encounter. We suggest several numerical improvements including the implicit derivative and stochastic gradient descent. We provide an extensive numerical study. Based both on the theoretical properties and numerical experiments, we conclude the paper by suggesting which method should be used in which situation.