Ute Spiske
An Investigation of Feature-based Nonrigid Image Registration using Gaussian Process
Jan 12, 2020
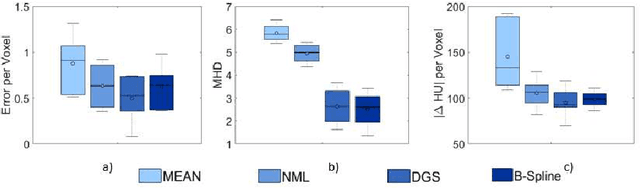
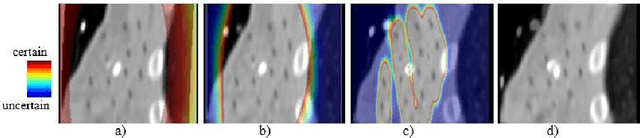
Abstract:For a wide range of clinical applications, such as adaptive treatment planning or intraoperative image update, feature-based deformable registration (FDR) approaches are widely employed because of their simplicity and low computational complexity. FDR algorithms estimate a dense displacement field by interpolating a sparse field, which is given by the established correspondence between selected features. In this paper, we consider the deformation field as a Gaussian Process (GP), whereas the selected features are regarded as prior information on the valid deformations. Using GP, we are able to estimate the both dense displacement field and a corresponding uncertainty map at once. Furthermore, we evaluated the performance of different hyperparameter settings for squared exponential kernels with synthetic, phantom and clinical data respectively. The quantitative comparison shows, GP-based interpolation has performance on par with state-of-the-art B-spline interpolation. The greatest clinical benefit of GP-based interpolation is that it gives a reliable estimate of the mathematical uncertainty of the calculated dense displacement map.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge