Ugur Akpinar
Wavefront Coding for Accommodation-Invariant Near-Eye Displays
Oct 14, 2025Abstract:We present a new computational near-eye display method that addresses the vergence-accommodation conflict problem in stereoscopic displays through accommodation-invariance. Our system integrates a refractive lens eyepiece with a novel wavefront coding diffractive optical element, operating in tandem with a pre-processing convolutional neural network. We employ end-to-end learning to jointly optimize the wavefront-coding optics and the image pre-processing module. To implement this approach, we develop a differentiable retinal image formation model that accounts for limiting aperture and chromatic aberrations introduced by the eye optics. We further integrate the neural transfer function and the contrast sensitivity function into the loss model to account for related perceptual effects. To tackle off-axis distortions, we incorporate position dependency into the pre-processing module. In addition to conducting rigorous analysis based on simulations, we also fabricate the designed diffractive optical element and build a benchtop setup, demonstrating accommodation-invariance for depth ranges of up to four diopters.
Generalized Tensor Summation Compressive Sensing Network (GTSNET): An Easy to Learn Compressive Sensing Operation
Aug 04, 2021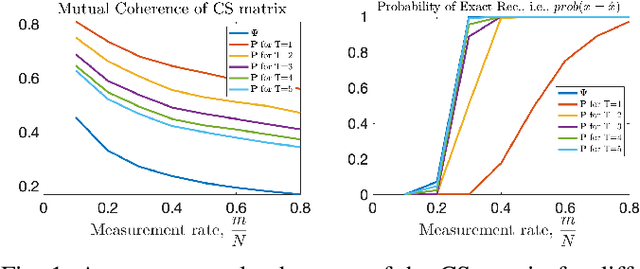


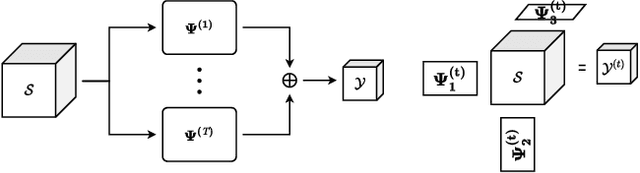
Abstract:In CS literature, the efforts can be divided into two groups: finding a measurement matrix that preserves the compressed information at the maximum level, and finding a reconstruction algorithm for the compressed information. In the traditional CS setup, the measurement matrices are selected as random matrices, and optimization-based iterative solutions are used to recover the signals. However, when we handle large signals, using random matrices become cumbersome especially when it comes to iterative optimization-based solutions. Even though recent deep learning-based solutions boost the reconstruction accuracy performance while speeding up the recovery, still jointly learning the whole measurement matrix is a difficult process. In this work, we introduce a separable multi-linear learning of the CS matrix by representing it as the summation of arbitrary number of tensors. For a special case where the CS operation is set as a single tensor multiplication, the model is reduced to the learning-based separable CS; while a dense CS matrix can be approximated and learned as the summation of multiple tensors. Both cases can be used in CS of two or multi-dimensional signals e.g., images, multi-spectral images, videos, etc. Structural CS matrices can also be easily approximated and learned in our multi-linear separable learning setup with structural tensor sum representation. Hence, our learnable generalized tensor summation CS operation encapsulates most CS setups including separable CS, non-separable CS (traditional vector-matrix multiplication), structural CS, and CS of the multi-dimensional signals. For both gray-scale and RGB images, the proposed scheme surpasses most state-of-the-art solutions, especially in lower measurement rates. Although the performance gain remains limited from tensor to the sum of tensor representation for gray-scale images, it becomes significant in the RGB case.
Learning Wavefront Coding for Extended Depth of Field Imaging
Dec 31, 2019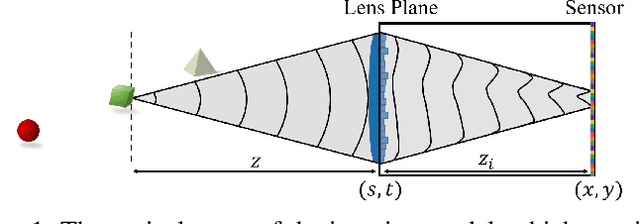

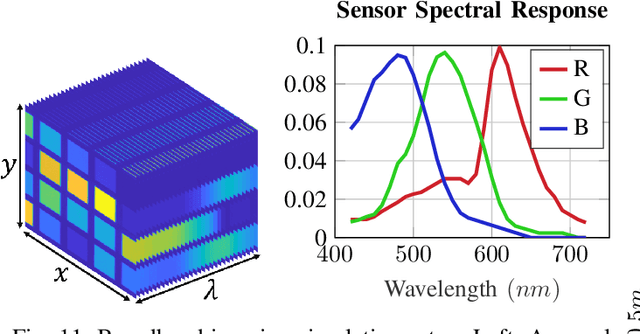

Abstract:The depth of field constitutes an important quality factor of imaging systems that highly affects the content of the acquired spatial information in the captured images. Extended depth of field (EDoF) imaging is a challenging problem due to its highly ill-posed nature, hence it has been extensively addressed in the literature. We propose a computational imaging approach for EDoF, where we employ wavefront coding via a diffractive optical element (DOE) and we achieve deblurring through a convolutional neural network. Thanks to the end-to-end differentiable modeling of optical image formation and computational post-processing, we jointly optimize the optical design, i.e., DOE, and the deblurring through standard gradient descent methods. Based on the properties of the underlying refractive lens and the desired EDoF range, we provide an analytical expression for the search space of the DOE, which helps in the convergence of the end-to-end network. We achieve superior EDoF imaging performance compared to state of the art, where we demonstrate results with minimal artifacts in various scenarios, including deep 3D scenes and broadband imaging.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge